Consider the following linear system: \[\overrightarrow{x}'=A(t)\overrightarrow{x}, \;\;\;\;(55)\] \(A(t)\) is a real-valued continuous function of \(t\).

Theorem. If \(\overrightarrow{x}=\overrightarrow{u}(t)+i\overrightarrow{v}(t)\) is a solution of (55) for real-valued functions \(\overrightarrow{u}(t)\) and \(\overrightarrow{v}(t)\), then so are \(\overrightarrow{u}(t)\) and \(\overrightarrow{v}(t)\).

Theorem. If \(A\) has complex eigenvalue \(\lambda=r+i\theta\) with corresponding eigenvector \(\overrightarrow{v}\), then two linearly independent solutions of (55) are \[\overrightarrow{x_1}=e^{rt}[\cos(\theta t)Re \overrightarrow{v}-\sin(\theta t)Im \overrightarrow{v}]\] and \[\overrightarrow{x_2}=e^{rt}[\cos(\theta t)Im \overrightarrow{v}+\sin(\theta t)Re \overrightarrow{v}].\]

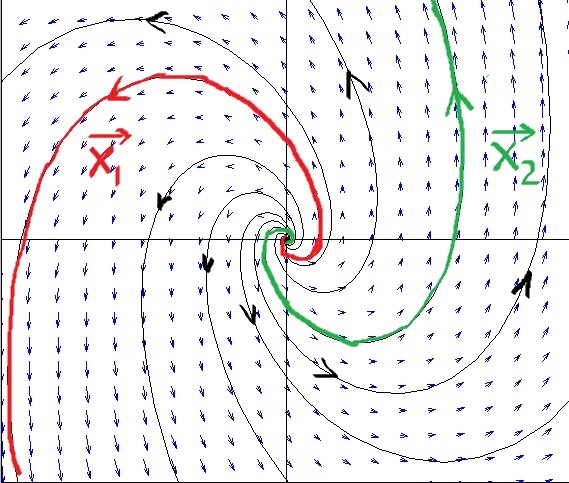
Example. \(\overrightarrow{x}'=\left[\begin{array}{rr} 1&-2\\5&3\end{array} \right] \overrightarrow{x}\).

1. Find the general solution.


2. Draw the phase portrait.

Solution. (a) \(\lambda=2\pm 3i\) and \(\overrightarrow{v}= \left[\begin{array}{l}-1+3i\\5\end{array} \right]\). A solution is \[\begin{align*} \overrightarrow{x}&=e^{2t}[\cos(3t)+i\sin(3t)] \left(\left[\begin{array}{r}-1\\5\end{array} \right] +i\left[\begin{array}{r}3\\0\end{array} \right]\right)\\ &=e^{2t}\left(\cos(3t)\left[\begin{array}{r}-1\\5\end{array} \right]-\sin(3t)\left[\begin{array}{r}3\\0\end{array} \right] \right)+ ie^{2t}\left(\cos(3t)\left[\begin{array}{r}3\\0\end{array} \right]+\sin(3t)\left[\begin{array}{r}-1\\5\end{array} \right]\right) \end{align*}\] So the general solution is \[\begin{align*} \overrightarrow{x}&=c_1 \overrightarrow{x_1} +c_2\overrightarrow{x_2}\\ &=c_1e^{2t}\left(\cos(3t)\left[\begin{array}{r}-1\\5\end{array} \right]-\sin(3t)\left[\begin{array}{r}3\\0\end{array} \right] \right)+ c_2e^{2t}\left(\cos(3t)\left[\begin{array}{r}3\\0\end{array} \right]+\sin(3t)\left[\begin{array}{r}-1\\5\end{array} \right]\right)\\ &=c_1e^{2t}\left[\begin{array}{l}-\cos(3t)-3\sin(3t)\\5\cos(3t)\end{array} \right]+ c_2e^{2t}\left[\begin{array}{r}3\cos(3t)- \sin(3t)\\5\sin(3t)\end{array} \right].\\ \end{align*}\] (b) To draw the spiral for \(\overrightarrow{x_1}\), get a point on it by plugging \(t=0\) and then find the tangent vector \(\overrightarrow{x_1}'(0)\) at the point \(\overrightarrow{x_1}(0)\). Do the same for \(\overrightarrow{x_2}\). The origin is an unstable spiral point. Note that the origin would have been an asymptotically stable spiral point if eigenvalues had negative real part.

Note that there are 3 types of trajectories for the eigenvalue \(\lambda=r\pm i \theta\) in a system of 2 linear ODEs:

1. \(r < 0\), the origin is an asymptotically stable spiral point


2. \(r > 0\), the origin is an unstable spiral point


3. \(r=0\), the origin is a stable center (trajectories are circle or ellipse)

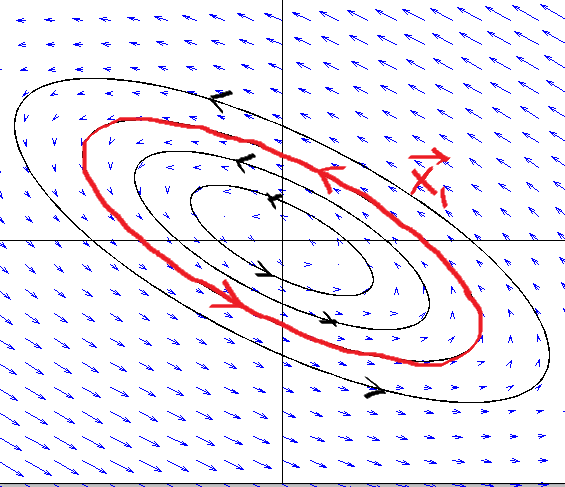
Example. \(\overrightarrow{x}'=\left[\begin{array}{rr} -1&-2\\1&1\end{array} \right] \overrightarrow{x}\).

1. Find the general solution.


2. Draw the phase portrait.

Solution. (a) \(\lambda=\pm i\) and \(\overrightarrow{v}= \left[\begin{array}{l}-1+i\\1\end{array} \right]\). A solution is \[\begin{align*} \overrightarrow{x}&=[\cos(t)+i\sin(t)] \left(\left[\begin{array}{r}-1\\1\end{array} \right] +i\left[\begin{array}{r}1\\0\end{array} \right]\right)\\ \end{align*}\] So the general solution is \[\begin{align*} \overrightarrow{x}&=c_1 \overrightarrow{x_1} +c_2\overrightarrow{x_2}\\ &=c_1\left(\cos(t)\left[\begin{array}{r}-1\\1\end{array} \right]-\sin(t)\left[\begin{array}{r}1\\0\end{array} \right] \right)+ c_2\left(\cos(t)\left[\begin{array}{r}1\\0\end{array} \right]+\sin(t)\left[\begin{array}{r}-1\\1\end{array} \right]\right)\\ &=c_1 \left[\begin{array}{l}-\cos t-\sin t\\\cos t\end{array} \right]+ c_2\left[\begin{array}{r}\cos t-\sin t\\\sin t\end{array} \right] \end{align*}\] (b) Let's draw the trajectory for \(\overrightarrow{x}=\overrightarrow{x_1}=\left[\begin{array}{l}-\cos t-\sin t\\\cos t\end{array} \right]\). It gives the trajectory \[x_1=-\cos t-\sin t,\; x_2=\cos t.\] Solving for \(\cos t\) and \(\sin t\), we get \(\sin t=-(x_1+x_2),\; \cos t=x_2\). Using \(\sin^2 t+\cos^2 t=1\), we get the trajectory which is the ellipse \[(x_1+x_2)^2+x_2^2=1\] whose one axis is \(x_1+x_2=0\). To determine the direction of a trajectory, plot tangent vector at a point, say \([1, \; 0]^T\): \[\overrightarrow{x}'=\left[\begin{array}{rr} -1&-2\\1&1\end{array} \right] \left[\begin{array}{r}1\\0\end{array} \right]=\left[\begin{array}{r}-1\\1\end{array} \right].\] So trajectories move counterclockwise. Note that if \(A\) is not given, then plug \(t=\pi/2\) to get a point \(\overrightarrow{x_1}(\pi/2)\) and the tangent vector \(\overrightarrow{x_1}'(\pi/2)\) at the point \(\overrightarrow{x_1}(\pi/2)\). The origin is a stable center, but not asymptotically stable as trajectories do not move toward the origin as \(t\) increases.

Last edited