Consider the following linear system:
\[\overrightarrow{x}'=A\overrightarrow{x}, \;\;\;\;(56)
\]
where \(A\) is a \(2\times 2\) real matrix. If \(A\) has two distinct eigenvalues, then there are two linearly independent
eigenvectors giving two linearly independent solution of (56). But if \(A\) has only one distinct eigenvalue
\(\lambda\) of multiplicity 2, then there is only one linearly independent eigenvector
\(\overrightarrow{v}\) giving only one linearly independent solution \(\overrightarrow{x}=e^{\lambda t}\overrightarrow{v}\)
of (56). It can be verified that \(\overrightarrow{x}=te^{\lambda t}\overrightarrow{v}\) is not a nonzero solution of (56).
Theorem. Suppose \(\lambda\) is an eigenvalue of a \(2\times 2\) real matrix \(A\) of multiplicity 2 with an
eigenvector \(\overrightarrow{v}\). Then the general solution of \(\overrightarrow{x}'=A\overrightarrow{x}\) is
\[\overrightarrow{x}=c_1e^{\lambda t}\overrightarrow{v}+c_2(te^{\lambda t}\overrightarrow{v}+e^{\lambda t}\overrightarrow{w}),\]
where \((A-\lambda I)\overrightarrow{w}=\overrightarrow{v}\)
or, equivalently \((A-\lambda I)^2\overrightarrow{w}=\overrightarrow{0}\). (\(\overrightarrow{w}\) is called
a generalized eigenvector of \(A\) corresponding the eigenvalue \(\lambda\))
First we show that \(\overrightarrow{x}=te^{\lambda t}\overrightarrow{v}+e^{\lambda t}\overrightarrow{w}\) is a solution
of \(\overrightarrow{x}'=A\overrightarrow{x}\).
\[\begin{align*}
LHS&=(te^{\lambda t}\overrightarrow{v}+e^{\lambda t}\overrightarrow{w})'=e^{\lambda t}\overrightarrow{v}+t\lambda e^{\lambda t}\overrightarrow{v}+\lambda e^{\lambda t}\overrightarrow{w}\\
RHS&=A(te^{\lambda t}\overrightarrow{v}+e^{\lambda t}\overrightarrow{w})=te^{\lambda t}A\overrightarrow{v}+e^{\lambda t}A\overrightarrow{w}
=te^{\lambda t}\lambda\overrightarrow{v}+e^{\lambda t}(\lambda\overrightarrow{w}+\overrightarrow{v}),
\end{align*}\]
since \((A-\lambda I)\overrightarrow{w}=\overrightarrow{v}\), i.e.,
\(A\overrightarrow{w}=\lambda\overrightarrow{w}+\overrightarrow{v}\). Thus \(LHS=RHS\).
Using Wronskian it can be shown that these two solutions are linearly independent.
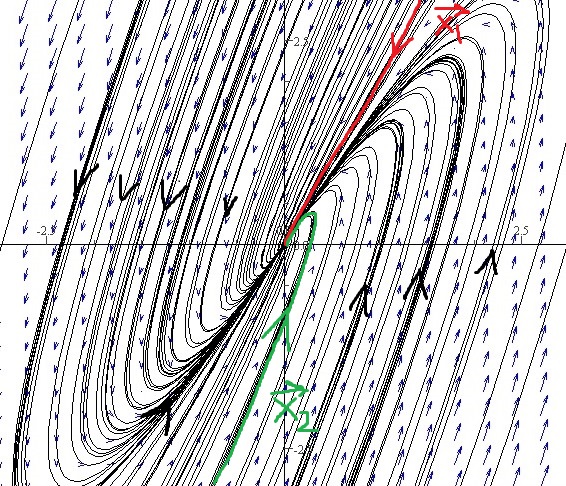
Solution. (a) The eigenvalues of the coefficient matrix are \(-1\) and \(-1\) with corresponding eigenvector
\(\overrightarrow{v}=\left[\begin{array}{r}1\\2\end{array} \right]\) (show all the steps).
Now let's find a vector \(\overrightarrow{w}\) that satisfies
\[\begin{align*}
&(A-\lambda I)\overrightarrow{w}=\overrightarrow{v}\\
\implies & \left[\begin{array}{rr}
2&-1\\4&-2\end{array} \right] \left[\begin{array}{r}w_1\\w_2\end{array} \right] = \left[\begin{array}{r}1\\2\end{array} \right]\\
\implies & \left[\begin{array}{r}2w_1-w_2\\4w_1-2w_2\end{array} \right] = \left[\begin{array}{r}1\\2\end{array} \right]\\
\implies & 2w_1-w_2=1\\
\implies & w_2=2w_1-1\\
\implies & \overrightarrow{w}=\left[\begin{array}{r}w_1\\w_2\end{array} \right] = \left[\begin{array}{l}w_1\\2w_1-1\end{array} \right] = w_1\left[\begin{array}{r}1\\2\end{array} \right] +\left[\begin{array}{r}0\\-1\end{array} \right]
\end{align*}\]
Assigning a particular value of \(w_1\), say \(w_1=0\), we get \(\overrightarrow{w}=\left[\begin{array}{r}0\\-1\end{array} \right]\).
So the general solution is
\[\overrightarrow{x}=c_1e^{-t}\left[\begin{array}{r}1\\2\end{array} \right]+c_2\left(te^{-t}\left[\begin{array}{r}1\\2\end{array} \right]+e^{-t}\left[\begin{array}{r}0\\-1\end{array} \right]\right).\]
(b) To draw the curve for \(\overrightarrow{x_2}\), get three points on it by plugging \(t=-1,0,1\).
The origin is called an improper node which is asymptotically stable when eigenvalues are negative
(trajectories move toward the origin as \(t\) increases) and unstable when eigenvalues are positive
(trajectories move away from the origin as \(t\) increases).
Note:
If \(\overrightarrow{x}'=A \overrightarrow{x}\) has a solution
\(\overrightarrow{x}_2=te^{-t}\left[\begin{array}{r}1\\2\end{array} \right]+e^{-t}\left[\begin{array}{r}0\\-1\end{array} \right]\)
where \(A\) is not given. Since \(\overrightarrow{x}_2(0)=\left[\begin{array}{r}0\\-1\end{array} \right]\),
the solution curve passes through \((0,-1)\). To find its direction at \((0,-1)\), find the tangent vector
\(\overrightarrow{x}'_2
=(1\cdot e^{-t}-te^{-t})\left[\begin{array}{r}1\\2\end{array} \right]-e^{-t}\left[\begin{array}{r}0\\-1\end{array} \right]
=\left[\begin{array}{r}1\\3\end{array} \right]\)
at \(t=0\).
