Suppose \(f\) is a continuous function on \([a,b]\). Suppose a particle is moving on the \(x\)-axis under a force field that exerts force \(f(x)\) when the particle is at \(x\). Then the work done \(W\) in moving the particle from \(x=a\) to \(x=b\) is \[W=\int_a^b f(x)\;dx.\]

Example. A force of \(\sin\left( \frac{\pi x}{4} \right)\) Newtons is acting on a particle moving on a line when it is \(x\) meters from the origin. How much work is required in moving the particle from \(x=1\) to \(x=9\)?

Solution. Here the force is \(f(x)=\sin\left( \frac{\pi x}{4} \right)\) N when the particle is \(x\) m from the origin on the \(x\)-axis. Thus required work is \[\int_1^9 \sin\left( \frac{\pi x}{4} \right)\;dx =\left.-\frac{4}{\pi}\cos\left( \frac{\pi x}{4} \right) \right\vert_1^9 =-\frac{4}{\pi}\cos\left( \frac{9\pi}{4} \right)+\frac{4}{\pi}\cos\left( \frac{\pi}{4} \right) =-\frac{4}{\pi\sqrt{2}}+\frac{4}{\pi\sqrt{2}}=0.\]

Now we discuss the problems of finding the work required to stretch or compress a spring.

Hooke's Law: The force \(f\) required to maintain a spring stretched or compressed \(x\) units beyond its natural length is \(f(x)=kx\) where \(k>0\) is the spring constant.

Suppose the natural length of a spring is \(x_0\) m and \(k\) is the spring constant. Then the work required to stretch it from \(x_1\) m to \(x_2\) m is \[\int_{x_1-x_0}^{x_2-x_0} f(x)\;dx =\int_{x_1-x_0}^{x_2-x_0} kx\;dx \;J,\] where \(J=Nm\).

Example. A spring has a natural length of \(20\) cm and \(15\) N force is required to keep it stretched to a length of \(25\) cm. How much work is required to stretch it from \(20\) cm to \(30\) cm?

Solution. Since \(15\) N force is required to stretch \(0.25-0.2=0.05\) m, by Hooke's Law, \[15=f(0.05)=k\cdot 0.05 \implies k=\frac{15}{0.05}=300 \;\text{N/m}.\] Then \(f(x)=300x\). The work required to stretch the spring from \(0.2\) m to \(0.3\) m is \[\int_{0.2-0.2}^{0.3-0.2} 300x\;dx=\int_0^{0.1} 300x\;dx=\left. 150x^2 \right\vert_0^{0.1}=1.5 \;J.\]

Now we discuss the problems of finding the work required to pump liquid out of a tank.

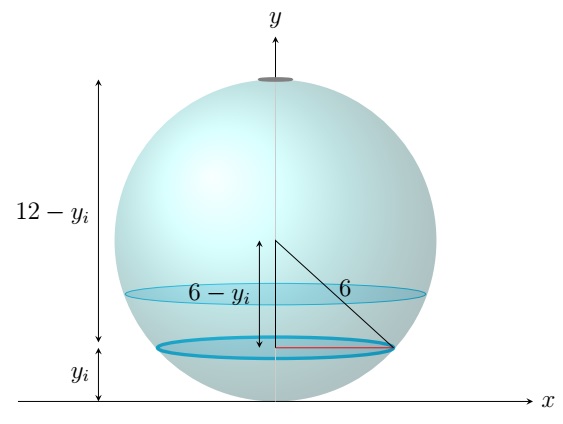
Example. Consider a spherical tank of radius \(6\) m. Suppose the tank is filled with a liquid with density \(1200\) kg/\(m^3\) to a height of \(4\) m. Find the work required to empty the tank through a whole at the top of the tank. Assume \(g=9.8\) m/s\(^2\).

Solution. First we approximate the required work \(W\) by approximating the work required to pump a thin layer of liquid to the top of the tank. Draw the origin at the bottom of the sphere and the \(y\)-axis vertically up through the center of the sphere.

Since the tank is filled to a height of \(4\) m, we partition the liquid into \(n\) layers by breaking \([0,4]\) into \(n\) subintervals \([y_0,y_1],[y_1,y_2],\ldots,[y_{n-1},y_n]\) where \(y_i=i \Delta y\) and \(\Delta y=4/n\). The \(i\)th layer of the liquid is approximately a circular cylinder of radius \(\sqrt{6^2-(6-y_i)^2}=\sqrt{12y_i-y_i^2}\) and height \(\Delta y\). So the volume \(V_i\) of the \(i\)th layer is \(V_i\approx \pi (12y_i-y_i^2) \Delta y\) and its mass \(m_i\) is \[m_i =1200V_i \approx 1200 \pi (12y_i-y_i^2) \Delta y.\]

The force \(f_i\) on the \(i\)th layer to overcome the gravitational force on it is \[f_i= m_i g \approx 9.8\cdot 1200 \pi (12y_i-y_i^2) \Delta y=11760 \pi (12y_i-y_i^2) \Delta y.\] Then the work \(W_i\) required in pumping the \(i\)th layer to the top of the tank is \[W_i\approx f_i(12-y_i) \approx 11760 \pi (12y_i-y_i^2)(12-y_i) \Delta y=11760 \pi (144y_i-24y_i^2+y_i^3) \Delta y.\] Therefore the total work \(W\) required is \[W= \sum_{i=1}^n W_i \approx \sum_{i=1}^n 11760 \pi (144y_i-24y_i^2+y_i^3) \Delta y.\] This approximation of \(W\) gets better as \(n\to \infty\). Thus \[\begin{align*} W=\lim_{n\to \infty} \sum_{i=1}^n 11760 \pi (144y_i-24y_i^2+y_i^3) \Delta y &=\int_0^4 11760 \pi (144y-24y^2+y^3)\;dy\\ &=11760 \pi\int_0^4 (144y-24y^2+y^3)\;dy\\ &=11760 \pi \left.\left(72y^2-8y^3+\frac{y^4}{4}\right) \right\vert_0^4\\ &=8279040 \pi \;J. \end{align*}\]

Last edited