Linear Homogeneous ODEs with Constant Coefficients |
In this section, we learn how to solve a linear homogeneous second order ODE with constant coefficients. \[a\frac{d^2y}{dx^2}+b\frac{dy}{dx}+cy=0, \text{ where } a\neq 0 \;\;\;\;(27)\] Suppose \(y=e^{rx}\) is a solution of (27) for some values of \(r\). Then \(y'=re^{rx}\) and \(y''=r^2e^{rx}\). Plugging these into (27), we get \[\begin{align*} ar^2e^{rx}+bre^{rx}+ce^{rx}&=0\\ e^{rx}(ar^2+br+c)&=0 \end{align*}\] Since \(e^{rx}\neq 0\), we get a quadratic equation in \(r\), called the characteristic equation of (27): \[ar^2+br+c=0 \;\;\;\;(28)\] There are three possibilities for the roots \(r_1\) and \(r_2\) of (28):
For this section assume that \(r_1\) and \(r_2\) are real and distinct. Then we have two solutions \(y=e^{r_1x}\)
and \(y=e^{r_2x}\) for (27). It can be verified that any of their linear combinations would also be a solution
of (27) (principle of superposition). Thus we get the general solution:
\[y=c_1e^{r_1x}+c_2e^{r_2x}\]
Now \(c_1\) and \(c_2\) can be found using two initial conditions as discussed before.
Steps to solve:
Example.
Find the general solution of the following ODE.
\[\frac{d^2y}{dx^2}-2\frac{dy}{dx}-3y=0\]
Solution. The characteristic equation is
\[\begin{align*}
r^2-2r-3&=0\\
(r+1)(r-3)&=0\\
r&=-1,3
\end{align*}\]
So the general solution is \[y=c_1e^{-x}+c_2e^{3x}.\]
Example.
Solve the following IVP.
\[2y''+5y'-3y=0,\;\; y(0)=11/7,\, y'(0)=-26/7\]
Solution. The characteristic equation is
\[\begin{align*}
2r^2+5r-3&=0\\
(2r-1)(r+3)&=0\\
r&=-3,1/2
\end{align*}\]
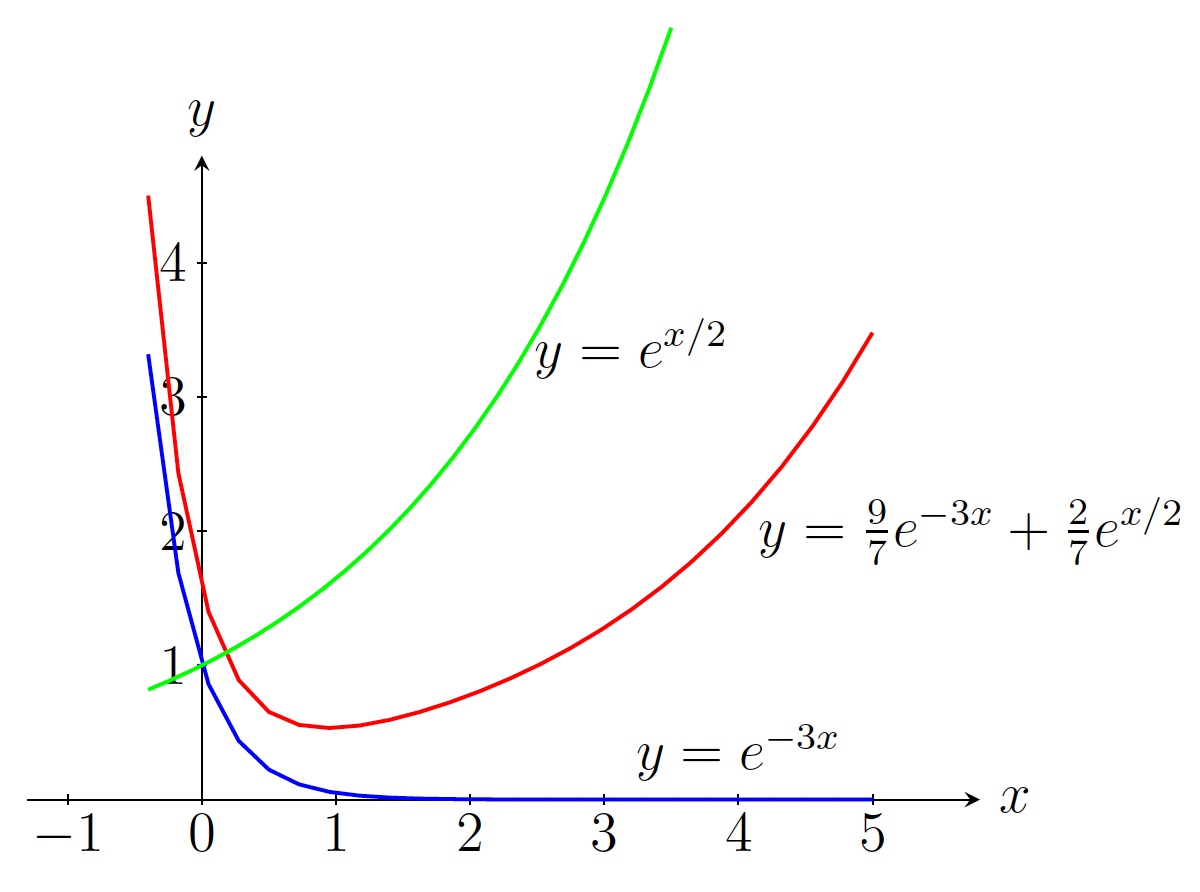
So the general solution is \[y=c_1e^{-3x}+c_2e^{x/2}.\]
Using the initial condition \(y(0)=11/7\), we get
\[c_1+c_2=11/7. \;\;\;\;(29)\]
Note that \(y'=-3c_1e^{-3x}+\frac{c_2}{2}e^{x/2}.\) Using the initial condition \(y'(0)=-26/7\), we get
\[-3c_1+c_2/2=-26/7. \;\;\;\;(30)\]
Solving (29) and (30), we get \(c_1=9/7\) and \(c_2=2/7\). Thus the solution of the IVP is
\[y=\frac{9}{7} e^{-3x}+\frac{2}{7} e^{x/2}.\]

Last edited