A sequence \(\{a_n\}\) of real numbers is a function \(f:\mathbb N\to \mathbb R\) such that \(f(n)=a_n\).
Sometimes it is denoted by \(\{a_n\}_{n=1}^{\infty}\) or by a few terms with a certain pattern \(\{a_1,a_2,a_3,\ldots\}\).
A sequence can also be defined recursively.
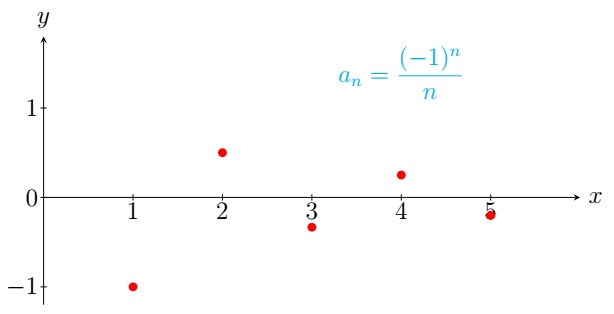
Example.
First four terms of the sequence \(\left\lbrace \frac{(-1)^n}{n}\right\rbrace\) are \(-1,\frac{1}{2},-\frac{1}{3},\frac{1}{4}\).
\(\{1,\frac{1}{2},\frac{1}{3},\frac{1}{4},\ldots\}\) can be written as \(\left\lbrace \frac{1}{n}\right\rbrace\).
The Fibonacci sequence \(\{F_n\}_{n=0}^{\infty}\) is defined by \[F_n=F_{n-1}+F_{n-2},\; n\geq 2,\; F_0=0,\; F_1=1.\]
Definition. A sequence \(\{a_n\}\) converges to a real number \(L\) if \(x_n\) can be made
arbitrarily close to \(L\) by taking sufficiently large \(n\) (for details, see the \(\varepsilon-N\) definition).
It is denoted by \(\displaystyle\lim_{n\to \infty} a_n=L\) or \(a_n\to L\) as \(n\to \infty\). The sequence
\(\{a_n\}\) diverges if it is not convergent.
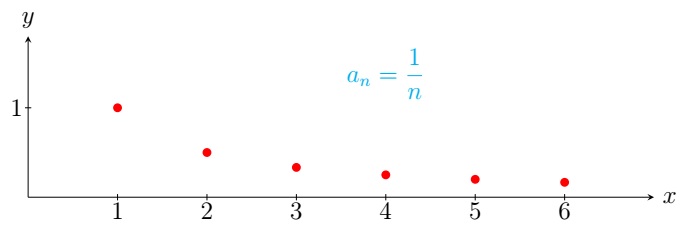
Example.
The sequence \(\left\lbrace \frac{1}{n}\right\rbrace\) converges to \(0\).
\(\{ n^2 \}\) diverges to \(\infty\).
\(\{(-1)^n\}\) diverges as its terms oscillate between \(1\) and \(-1\).
Note that if a sequence \(\{x_n\}\) diverges, its terms oscillate indefinitely like that of \(\{(-1)^n\}\) or
it diverges to \(\pm \infty\).
Theorem.
If \(a_n=f(n)\) for all integers \(n\geq 1\) and \(\displaystyle\lim_{x\to \infty} f(x)=L\), then \(\displaystyle\lim_{n\to \infty} a_n=L\).
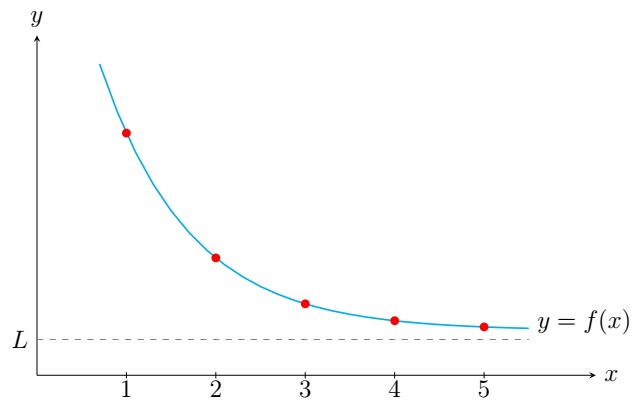
Example.
Show that \(\displaystyle\lim_{n\to \infty} \frac{n+\tan^{-1}n}{n}=1\).
Solution. Let \(f(x)=\displaystyle\frac{x+\tan^{-1}x}{x}\). Note that \(f(n)\) is the \(n\)th term
of the sequence \(\left\lbrace \displaystyle\frac{n+\tan^{-1}n}{n} \right\rbrace\).
\[ \displaystyle\lim_{x\to \infty} f(x)=
\displaystyle\lim_{x\to \infty} \frac{x+\tan^{-1}x}{x}
= \displaystyle\lim_{x\to \infty} \frac{1+\frac{1}{1+x^2}}{1} =1
\;\;\left(\text{by l'Hospitals's Rule} \right). \]
Thus \(\displaystyle\lim_{n\to \infty} \frac{n+\tan^{-1}n}{n}=1\), i.e., the sequence
\(\left\lbrace \displaystyle \frac{n+\tan^{-1}n}{n} \right\rbrace\) converges to \(1\).
Algebra of limits for sequences: Theorem.
The following are true for any convergent sequences \(\{a_n\}\) and \(\{b_n\}\):
\(\displaystyle\lim_{n\to \infty} a_n^p=\left(\displaystyle\lim_{n\to \infty} a_n \right)^p\) for all real numbers \(p>0\) whenever \(a_n>0\).
Note that the convergence in the assumption is crucial. For \(\{a_n\}=\{\frac{1}{n}\}\) and \(\{b_n\}=\{n\}\),
we have \(\{a_nb_n\}=\{1\}\). But
\[\displaystyle\lim_{n\to \infty} a_nb_n=1\neq 0\cdot \infty\ =\left(\displaystyle\lim_{n\to \infty} a_n \right) \left(\displaystyle\lim_{n\to \infty} b_n\right).\]
Example.
Determine if the sequence \(\{a_n\}\) converges or diverges.
(a) \(a_n=\displaystyle\frac{n^3}{n^3+1}\), (b) \(a_n=\displaystyle\frac{n^3}{n+1}\), (c) \(a_n=\displaystyle\sqrt{\frac{n+1}{9n+1}}\).
Theorem.
If \(\{a_n\}\) is convergent and \(f\) is a continuous function, then
\[\displaystyle\lim_{n\to \infty} f(a_n)=f\left( \displaystyle\lim_{n\to \infty} a_n \right).\]
Example.
Since \(f(x)=\cos x\) is a continuous function,
\[\displaystyle\lim_{n\to \infty} \cos\left( \frac{2}{n} \right)=\cos\left( \displaystyle\lim_{n\to \infty} \frac{2}{n} \right)=\cos 0=1.\]
Thus \(\left\lbrace \cos\left( \frac{2}{n} \right) \right\rbrace\) converges to \(1\).
Theorem.(Sandwich Theorem)
Suppose \(a_n\leq b_n\leq c_n\) for all natural numbers \(n\). If both \(\{a_n\}\) and \(\{c_n\}\) converge to
\(L\), then \(\{b_n\}\) also converges to \(L\).
Example.
Show that \(\displaystyle\lim_{n\to \infty} \frac{\sin(3n)}{n}=0\).
Solution. First note that \(-1\leq \sin(3n) \leq 1\) for all real numbers \(n\). Then for all natural
numbers \(n\),
\[-\frac{1}{n}\leq \frac{\sin(3n)}{n} \leq \frac{1}{n}.\]
Since \(\displaystyle\lim_{n\to \infty} \frac{-1}{n}=\displaystyle\lim_{n\to \infty} \frac{1}{n}=0\), we have
\(\displaystyle\lim_{n\to \infty} \frac{\sin(3n)}{n}=0\) by the Sandwich Theorem.
As consequences of the Sandwich Theorem, we have the following results:
If \(\displaystyle\lim_{n\to \infty} |a_n|=0\), then \(\displaystyle\lim_{n\to \infty} a_n=0\).
\(\left\lbrace r^n \right\rbrace\) is convergent if \(-1< r\leq 1\) and divergent otherwise.
In particular,
\[ \lim_{n\to \infty} r^n= \begin{cases}
0 & \text{if } -1< r <1 \\
1 & \text{if } r=1.
\end{cases}
\]
(a) \(-|a_n|\leq a_n \leq |a_n|\) for all natural numbers \(n\). Now apply the Sandwich Theorem.
(b) If \(r=1\), then \(\left\lbrace r^n \right\rbrace=\{1\}\) is convergent. Suppose \(-1< r< 1\).
Then \(0\leq |r|< 1\). Since \(\displaystyle\lim_{x\to \infty} |r|^x=0\),
\(\displaystyle\lim_{n\to \infty} |r|^n=0\). Since \(|r|^n=|r^n|\), \(\displaystyle\lim_{n\to \infty} r^n=0\)
by (a).
For \(r>1\), \(\displaystyle\lim_{x\to \infty} r^x=\infty\) and hence \(\displaystyle\lim_{n\to \infty} r^n=\infty\).
For \(r=-1\), note that \(\{(-1)^n\}\) is divergent as its terms oscillate between \(1\) and \(-1\).
Similar arguments can be applied for \(r<-1\).
(b) \(\displaystyle\lim_{n\to \infty} \frac{2^n(-1)^n}{3^n}=\displaystyle\lim_{n\to \infty} \left( -\frac{2}{3} \right)^n=0\)
as \(-1<-\frac{2}{3}\leq 1\). But \(\displaystyle\lim_{n\to \infty} \left(\frac{3}{2} \right)^n\) does not exist as
\(\frac{3}{2}>1\).
Definition.
A sequence \(\{a_n\}\) is bounded if there exists a real number \(M\) such that \(|a_n|\leq M\) for
all natural numbers \(n\).
Example.
\(\{\frac{1}{n}\}\) is bounded since \(|\frac{1}{n}|\leq 1\) for all natural numbers \(n\).
Theorem.
A convergent sequence is bounded.
Definition.
A sequence \(\{a_n\}\) is increasing if \(a_{n+1} > a_n\) for all natural numbers \(n\) and
decreasing if \(a_{n+1}< a_n\) for all natural numbers \(n\).
Theorem.(Monotone Convergence Theorem)
An increasing sequence that is bounded above is convergent.
A decreasing sequence that is bounded below is convergent.
Note that the Monotone Convergence Theorem is also true for non-decreasing and non-increasing sequences respectively.
Example.
\(\{\frac{1}{n}\}\) is a decreasing sequence as \(a_{n+1}=\frac{1}{n+1}<\frac{1}{n}=a_n\) for
all natural numbers \(n\). Also \(\{\frac{1}{n}\}\) is bounded below by \(0\) as \(0<\frac{1}{n}=a_n\)
for all natural numbers \(n\). Since \(\{\frac{1}{n}\}\) is decreasing and bounded below, it is convergent by
the Monotone Convergence Theorem.
\(\{x_n\}\) where \(x_1=\sqrt{2}\) and \(x_n=\sqrt{2+x_{n-1}},\;n\geq 2\).
We show \(\{x_n\}\) is increasing by induction. First note that
\[x_1=\sqrt{2}< \sqrt{2+\sqrt{2}}=\sqrt{2+x_1}=x_2.\]
Assume \(x_{n-1}< x_n\) for some \(n\in \mathbb N\). We show \(x_{n} < x_{n+1}\). Note that
\[\begin{align*}
& x_{n+1}^2-x_n^2=(2+x_n)-(2+x_{n-1})=x_n-x_{n-1}\\
\implies & x_{n+1}-x_n=(x_n-x_{n-1})/(x_{n+1}+x_n)
\end{align*}\]
Since \(x_{n-1} < x_n\) and \(x_n,x_{n+1} > 0\), we have \(x_{n+1}-x_n=(x_n-x_{n-1})/(x_{n+1}+x_n) > 0\), i.e.,
\(x_{n} < x_{n+1}\).
We show \(\{x_n\}\) is bounded above also by induction. Note that \(x_1=\sqrt{2}<3\) and \(x_2=\sqrt{2+\sqrt{2}}<3\).
Assume \( x_n < 3 \) for some \(n\in \mathbb N\). We show \( x_{n+1} < 3 \). Note that
\[x_{n+1}=\sqrt{2+x_n}<\sqrt{2+3} < 3.\]
By mathematical induction \(x_n < 3\) for all natural numbers \(n\).
Since \(\{x_n\}\) is an increasing sequence bounded above by \(3\), it is convergent by the MCT. Suppose
\(\displaystyle\lim_{n\to \infty} x_n=L\). To find \(L\), note that \(x_n^2=2+x_{n-1},\;n\geq 2.\) Taking limit
of both sides we get
\[\displaystyle\lim_{n\to \infty} x_n^2=\displaystyle\lim_{n\to \infty} (2+x_{n-1}) \implies (\displaystyle\lim_{n\to \infty} x_n)^2=2+ \displaystyle\lim_{n\to \infty} x_{n-1} \implies L^2=2+L \implies L=-1,2.\]
Since \(x_n>0\) for all natural numbers \(n\), \(L\geq 0\). Thus \(L=2\), i.e., \(\displaystyle\lim_{n\to \infty} x_n=2\).
