LearnMathOnline

Consider the following problem:
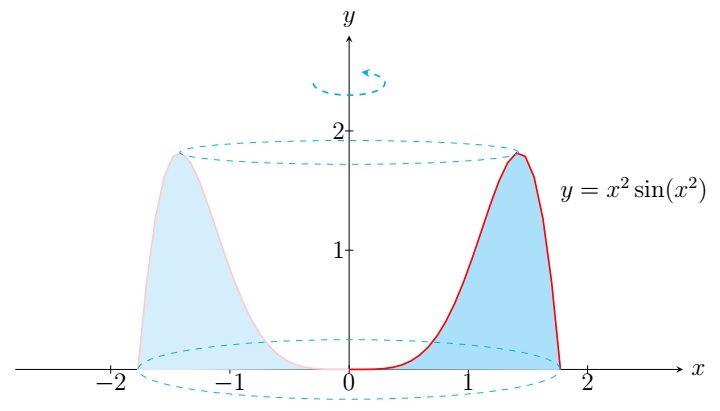
Find the volume of the solid obtained by rotating the region bounded by \(y=x^2\sin(x^2)\), \(x=0\), \(x=\sqrt{\pi}\), and \(y=0\) about the \(y\)-axis.

First note that the cross-section of the solid at \(y\) perpendicular to the \(y\)-axis is a washer. To apply the washer method, we need to find the inner radius and the outer radius which will require to solve for \(x\) in terms of \(y\) from \(y=x^2\sin(x^2)\). It is complicated and sometimes analytically impossible to solve for \(x\) in terms of \(y\) from \(y=f(x)\). We have a better method for this kind of problems:

Cylindrical Shells Method:
Consider the region bounded by \(y=f(x)\), \(x=a\), \(x=b\), and the \(x\)-axis. If \(S\) is the solid obtained by rotating the region about the \(y\)-axis, then the volume of \(S\) is \[V(S)= \int_a^b 2\pi x f(x)\;dx.\] We can remember the preceding formula by associating \(2\pi x,\; f(x)\), and \(dx\) with the circumference, height, and thickness of the cylindrical shell with the radius \(x\) respectively.

Break \([a,b]\) into \(n\) subintervals \([x_0,x_1],[x_1,x_2],\ldots,[x_{n-1},x_n]\) where \(x_i=a+i \Delta x\) and \(\Delta x=(b-a)/n\). Partition \(S\) into \(n\) solids \(S_1,S_2,\ldots,S_n\) by intersecting \(S\) by the vertical planes at \(x_1,x_2,\ldots,x_{n-1}\). Then the volume of \(S_i\) is approximately that of the cylindrical shell with the inner radius \(x_{i-1}\), the outer radius \(x_i\), and height \(f(x_i^*)\) where \(x_i^*=\frac{x_{i-1}+x_i}{2}\), \(i=1,2,\ldots,n\). Therefore \[\begin{align*} V(S_i) &\approx \pi x_i^2 f(x_i^*)-\pi x_{i-1}^2 f(x_i^*)\\ &=\pi f(x_i^*)\left( x_i^2 -x_{i-1}^2\right)\\ &=\pi f(x_i^*) (x_i+x_{i-1})(x_i-x_{i-1})\\ &=2\pi f(x_i^*) \frac{x_{i-1}+x_i}{2} (x_i-x_{i-1})\\ &=2\pi f(x_i^*) x_i^* \Delta x. \end{align*}\] Thus the volume of \(S\) is \[V(S)\approx \sum_{i=1}^n 2\pi x_i^* f(x_i^*) \Delta x.\] This approximation of \(V(S)\) gets better as \(n\to \infty\). Thus \[V(S)=\lim_{n\to \infty} \sum_{i=1}^n 2\pi x_i^* f(x_i^*) \Delta x=\int_a^b 2\pi x f(x)\;dx.\]

Example. Find the volume of the solid obtained by rotating the region bounded by \(y=x^2\sin(x^2)\), \(x=0\), \(x=\sqrt{\pi}\), and \(y=0\) about the \(y\)-axis.

Solution.

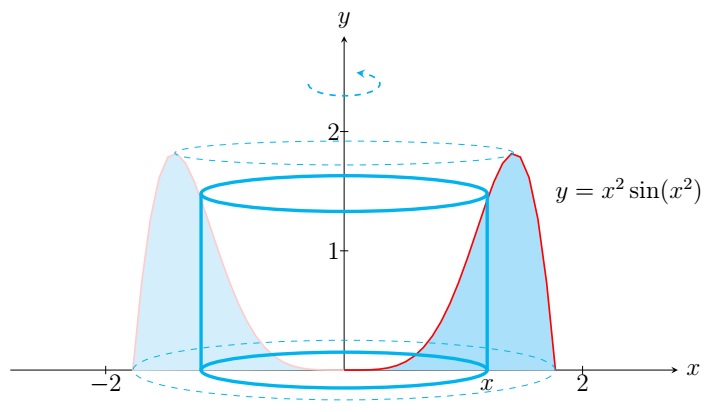
The volume of the solid is \[\begin{align*} & \int_0^{\sqrt{\pi}} 2\pi x\cdot x^2\sin(x^2)\;dx \\ =\;& \pi\int_0^{\sqrt{\pi}} x^2\sin(x^2) \cdot 2x\;dx \\ =\;& \pi\int_0^{\pi} u\sin u\;du \;\;\left( \text{Let } u=x^2. \text{ Then } du=2x\;dx\right) \\ =\;& \pi \left.\left( -u\cos u +\sin u \right)\right\vert_0^{\pi} \;\;\left( \text{Integrating by parts} \right) \\ =\;& \pi \left( -\pi\cos \pi +\sin \pi \right) -\pi \left( -0\cos 0 +\sin 0 \right) \\ =\;& \pi^2. \end{align*}\]

For some problems, the formula of Cylindrical Shells Method \(V(S)= \int_a^b 2\pi x f(x)\;dx\) is modified by replacing \(x\) and \(f(x)\) by the radius and the height of the cylindrical shell at \(x\) respectively.

Example. Find the volume of the solid obtained by rotating the region bounded by \(y=x\) and \(y=\frac{2x}{x^3+1}\) about the line \(x=-1\).

Solution.

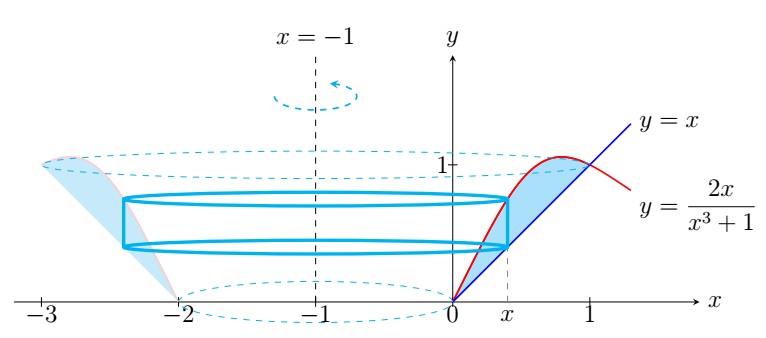
First note that \(y=x\) and \(y=\frac{2x}{x^3+1}\) intersect at \(x=0,1\). The cylindrical shell at \(x\) has radius \(x-(-1)\) and height \(\frac{2x}{x^3+1}-x\). The volume of the solid is \[\begin{align*} & \int_0^1 2\pi (x+1) \left( \frac{2x}{x^3+1} -x\right)\;dx \\ =\;& 2\pi\int_0^1 \left[-(x+1)x+(x+1)\frac{2x}{x^3+1} \right]\;dx\\ =\;& 2\pi\int_0^1 \left[-x^2-x+\frac{2x}{x^2-x+1} \right]\;dx\\ =\;& 2\pi\int_0^1 \left[-x^2-x+\frac{2x-1}{x^2-x+1} +\frac{1}{\left(x-\frac{1}{2}\right)^2+\left( \frac{\sqrt{3}}{2} \right)^2} \right]\;dx\\ =\;& 2\pi \left.\left( -\frac{x^3}{3}-\frac{x^2}{2}+\ln|x^2-x+1|+\frac{2}{\sqrt{3}}\tan^{-1}\left(\frac{x-\frac{1}{2}}{\frac{\sqrt{3}}{2}} \right) \right)\right\vert_0^1 \\ =\;& 2\pi\left( -\frac{5}{6}+\frac{4}{\sqrt{3}} \tan^{-1}\left( \frac{1}{\sqrt{3}} \right) \right)\\ =\;& 2\pi\left( -\frac{5}{6}+\frac{2\pi}{3\sqrt{3}} \right). \end{align*}\]

The roles of \(x\) and \(y\) in the Cylindrical Shells Method may be switched for some problems.

Example. Find the volume of the solid obtained by rotating the region bounded by \(x=y(3-e^y)\) and the \(y\)-axis about the \(x\)-axis.

Solution. First note that at the points of intersection of \(x=y(3-e^y)\) and \(x=0\), we have \[ y(3-e^y)=0\implies y=0,\ln 3. \] The cylindrical shell at \(y\) has radius \(y\) and height \(y(3-e^y)\). The volume of the solid is \[\begin{align*} & \int_0^{\ln 3} 2\pi y \cdot y(3-e^y) \;dy\\ =\;& 2\pi\int_0^{\ln 3} \left(3y^2-y^2e^y \right) \;dy\\ =\;& 2\pi \left.\left(y^3-e^y(y^2-2y+2) \right) \right\vert_0^{\ln 3} \;\;\left( \text{Integrating by parts} \right) \\ =\;& 2\pi \left((\ln 3)^3-3((\ln 3)^2-2\ln 3+2) \right)+4\pi\\ =\;& 2\pi \left((\ln 3)^3-3(\ln 3)^2+6\ln 3-4) \right). \end{align*}\]