Suppose \(B=\left(\overrightarrow{b_1},\ldots, \overrightarrow{b_n}\right)\) is an ordered basis of \(\mathbb R^n\). Then any vector \(\overrightarrow{x}\in \mathbb R^n\) can be written as \(\overrightarrow{x}=c_1\overrightarrow{b_1}+c_2\overrightarrow{b_2}+\cdots+c_n\overrightarrow{b_n}\) for some unique scalars \(c_1,c_2,\ldots,c_n\). The coordinate vector of \(\overrightarrow{x}\) relative to \(B\) or the \(B\)-coordinate of \(\overrightarrow{x}\), denoted by \([\overrightarrow{x}]_B\), is \([\overrightarrow{x}]_B=\left[c_1,c_2, \ldots,c_n \right]^T\).

Example.

1. For \(E_2=\left(\overrightarrow{e_1},\overrightarrow{e_2}\right)\) and \(\overrightarrow{x}=[3,2]^T=3\overrightarrow{e_1}+2\overrightarrow{e_2}\), we have \([\overrightarrow{x}]_{E_2}=\left[3,2 \right]^T\).


2. For \(B=\left(\overrightarrow{e_1}, \overrightarrow{e_1}+2\overrightarrow{e_2} \right)\) and \(\overrightarrow{x}=[3,2]^T=2\overrightarrow{e_1}+1(\overrightarrow{e_1}+2\overrightarrow{e_2})\), we have \([\overrightarrow{x}]_{B}=\left[2,1 \right]^T\).

Remark. \([\;\;]_B\) is an isomorphism on \(\mathbb R^n\).

For two ordered bases \(B=\left(\overrightarrow{b_1},\ldots, \overrightarrow{b_n}\right)\) and \(C=\left(\overrightarrow{c_1},\ldots, \overrightarrow{c_n}\right)\) of \(\mathbb R^n\), what is the relationship between \([\overrightarrow{x}]_B\) and \([\overrightarrow{x}]_C\)?
The change of basis matrix from \(B\) to \(C\), denoted by \(M_{C\leftarrow B}\), is the \(n\times n\) invertible matrix for which \([\overrightarrow{x}]_C=M_{C\leftarrow B}[\overrightarrow{x}]_B\) for all \(\overrightarrow{x}\in \mathbb R^n\). How to find \(M_{C\leftarrow B}\)?

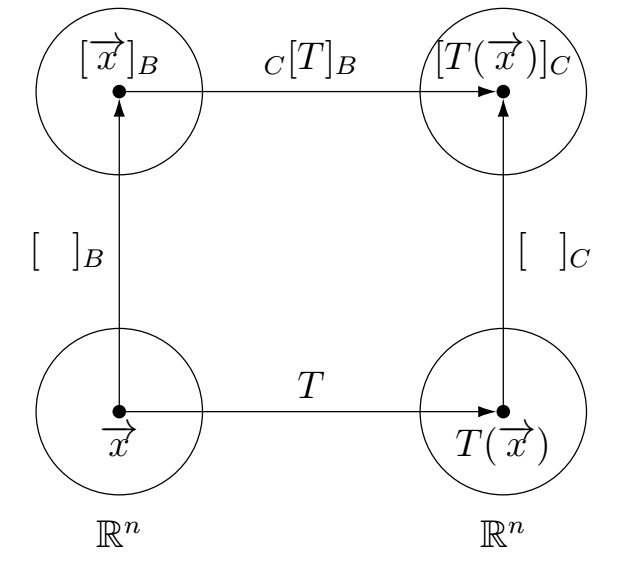
Let \(A\) be an \(n\times n\) matrix. Consider the linear transformations \(T:\mathbb R^n\to \mathbb R^n\) defined by \(T(\overrightarrow{x})=A\overrightarrow{x}\). So \(T\) is the matrix transformation \(\overrightarrow{x} \mapsto A\overrightarrow{x}\). Consider two ordered bases \(B=\left(\overrightarrow{b_1},\ldots, \overrightarrow{b_n}\right)\) and \(C=\left(\overrightarrow{c_1},\ldots, \overrightarrow{c_n}\right)\) of \(\mathbb R^n\). What is the relationship between \([\overrightarrow{x}]_B\) and \([T(\overrightarrow{x})]_C\)?
The matrix of \(T\) from \(B\) to \(C\), denoted by \([T]_{C\leftarrow B}\) or \(_{C}[T]_B\), is the \(n\times n\) invertible matrix for which \([T(\overrightarrow{x})]_C=_{C}[T]_B [\overrightarrow{x}]_B\) for all \(\overrightarrow{x}\in \mathbb R^n\). How to find \(_{C}[T]_B\)?

For a vector \(\overrightarrow{x}\in \mathbb R^n\), suppose \([\overrightarrow{x}]_B=\left[r_1,r_2, \ldots,r_n \right]^T\), i.e., \(\overrightarrow{x}=r_1\overrightarrow{b_1}+\cdots+r_n\overrightarrow{b_n}\). Then \[T(\overrightarrow{x})=A\overrightarrow{x}=A(r_1\overrightarrow{b_1}+\cdots+r_n\overrightarrow{b_n})=r_1A\overrightarrow{b_1}+\cdots+r_nA\overrightarrow{b_n}.\] \[\begin{align*} [A\overrightarrow{x}]_C &= [r_1A\overrightarrow{b_1}+\cdots+r_nA\overrightarrow{b_n}]_C\\ &= r_1[A\overrightarrow{b_1}]_C+\cdots+r_n[A\overrightarrow{b_n}]_C\\ &=\left[ [A\overrightarrow{b_1}]_C \cdots [A\overrightarrow{b_n}]_C\right] \left[\begin{array}{c}r_1\\ \vdots\\r_n\end{array} \right]\\ &=\left[ [A\overrightarrow{b_1}]_C \cdots [A\overrightarrow{b_n}]_C\right] [\overrightarrow{x}]_B. \end{align*}\] Thus \[_{C}[T]_B=\left[ [A\overrightarrow{b_1}]_C \cdots [A\overrightarrow{b_n}]_C\right].\]
Remark.

1. If \(C=B\), then we simply denote \(_{C}[T]_B\) by \([T]_B\), called the \(B\)-matrix of \(T:\overrightarrow{x} \mapsto A\overrightarrow{x}\).


2. If \(B=\{\overrightarrow{e_1},\ldots, \overrightarrow{e_n} \}\), then \([T]_B=A\), the standard matrix of \(T:\overrightarrow{x} \mapsto A\overrightarrow{x}\).


3. If \(A=I_n\), then \(T=I\) and \(_{C}[I]_B=M_{C\leftarrow B}\), the change of basis matrix from \(B\) to \(C\).

Example. Let \(B=\left( \left[\begin{array}{c}1\\0\end{array}\right],\; \left[\begin{array}{c}1\\1\end{array}\right] \right)\), \(C=\left(\left[\begin{array}{c}1\\2\end{array}\right],\; \left[\begin{array}{c}3\\1\end{array}\right] \right)\), and \(A=\left[\begin{array}{rr}-2&7\\1&4\end{array} \right]\).

1. Find \(_{C}[T]_B\), the matrix of \(T:\overrightarrow{x} \mapsto A\overrightarrow{x}\) from \(B\) to \(C\) and use it to find \([T(\overrightarrow{x})]_C\) where \([\overrightarrow{x}]_B=[13,-1]^T\).


2. Find \([T]_B\), the \(B\)-matrix of \(T:\overrightarrow{x} \mapsto A\overrightarrow{x}\).


3. Find \(M_{C\leftarrow B}\), the change of basis matrix from \(B\) to \(C\) and use it to find \([\overrightarrow{x}]_C\) where \([\overrightarrow{x}]_B=[13,-1]^T\).

Solution. (a) \[\begin{align*} A\overrightarrow{b_1} &= \left[\begin{array}{r}-2\\1\end{array}\right] =1 \left[\begin{array}{c}1\\2\end{array}\right] -1 \left[\begin{array}{c}3\\1\end{array}\right] =1\overrightarrow{c_1}-1\overrightarrow{c_2} \implies [A\overrightarrow{b_1}]_C =\left[\begin{array}{r}1\\-1\end{array}\right]\\ A\overrightarrow{b_2} &= \left[\begin{array}{c}5\\5\end{array}\right] =2 \left[\begin{array}{c}1\\2\end{array}\right] +1 \left[\begin{array}{c}3\\1\end{array}\right] =2\overrightarrow{c_1}+1\overrightarrow{c_2} \implies [A\overrightarrow{b_2}]_C =\left[\begin{array}{r}2\\1\end{array}\right] \end{align*}\] So the matrix of \(T:\overrightarrow{x} \mapsto A\overrightarrow{x}\) from \(B\) to \(C\) is \[_{C}[T]_B=\left[[A\overrightarrow{b_1}]_C\; [A\overrightarrow{b_2}]_C \right] =\left[\begin{array}{rr}1&2\\-1&1\end{array}\right].\] \[[T(\overrightarrow{x})]_C=_{C}[T]_B[\overrightarrow{x}]_B =\left[\begin{array}{rr}1&2\\-1&1\end{array}\right] \left[\begin{array}{r}13\\-1\end{array}\right] =\left[\begin{array}{r}11\\-14\end{array}\right].\] (b) \[\begin{align*} A\overrightarrow{b_1} &= \left[\begin{array}{r}-2\\1\end{array}\right] =-3 \left[\begin{array}{c}1\\0\end{array}\right] +1 \left[\begin{array}{c}1\\1\end{array}\right] =-3\overrightarrow{b_1}+1\overrightarrow{b_2} \implies [A\overrightarrow{b_1}]_B =\left[\begin{array}{r}-3\\1\end{array}\right]\\ A\overrightarrow{b_2} &= \left[\begin{array}{c}5\\5\end{array}\right] =0 \left[\begin{array}{c}1\\0\end{array}\right] +5 \left[\begin{array}{c}1\\1\end{array}\right] =0\overrightarrow{b_1}+5\overrightarrow{b_2} \implies [A\overrightarrow{b_2}]_B =\left[\begin{array}{r}0\\5\end{array}\right] \end{align*}\] So the \(B\)-matrix of \(T:\overrightarrow{x} \mapsto A\overrightarrow{x}\) is \[[T]_B=\left[[A\overrightarrow{b_1}]_B\; [A\overrightarrow{b_2}]_B \right] =\left[\begin{array}{rr}-3&0\\1&5\end{array}\right].\] (c) \[\begin{align*} \overrightarrow{b_1} &= \left[\begin{array}{c}1\\0\end{array}\right] =-\frac{1}{5} \left[\begin{array}{c}1\\2\end{array}\right] +\frac{2}{5}\left[\begin{array}{c}3\\1\end{array}\right] =-\frac{1}{5}\overrightarrow{c_1}+\frac{2}{5}\overrightarrow{c_2} \implies [\overrightarrow{b_1}]_C =\left[\begin{array}{r}-\frac{1}{5}\\\frac{2}{5}\end{array}\right]\\ \overrightarrow{b_2} &= \left[\begin{array}{c}1\\1\end{array}\right] =\frac{2}{5} \left[\begin{array}{c}1\\2\end{array}\right] +\frac{1}{5} \left[\begin{array}{c}3\\1\end{array}\right] =\frac{2}{5}\overrightarrow{c_1}+\frac{1}{5}\overrightarrow{c_2} \implies [\overrightarrow{b_2}]_C =\left[\begin{array}{r}\frac{2}{5}\\\frac{1}{5}\end{array}\right] \end{align*}\] So the change of basis matrix from \(B\) to \(C\) is \[M_{C\leftarrow B}=_{C}[I]_B=\left[[\overrightarrow{b_1}]_C\; [\overrightarrow{b_2}]_C \right]= \left[\begin{array}{rr}-\frac{1}{5}&\frac{2}{5}\\\frac{2}{5}&\frac{1}{5}\end{array}\right] =\frac{1}{5} \left[\begin{array}{rr}-1&2\\2&1\end{array}\right].\] \[[\overrightarrow{x}]_C=M_{C\leftarrow B}[\overrightarrow{x}]_B =\frac{1}{5} \left[\begin{array}{rr}-1&2\\2&1\end{array}\right] \left[\begin{array}{r}13\\-1\end{array}\right] =\left[\begin{array}{r}-3\\5\end{array}\right].\]

Theorem. Let \(A\) and \(D\) be two \(n\times n\) matrices such that \(A=PDP^{-1}\). If \(B\) is the basis of \(\mathbb R^n\) formed from the columns of \(P\), then the \(B\)-matrix of \(\overrightarrow{x} \mapsto A\overrightarrow{x}\) is \(D=P^{-1}AP\).

Remark.

1. Suppose \(A\) is diagonalizable and \(A=PDP^{-1}\) where \(D\) is a diagonal matrix. If \(B\) is the basis of \(\mathbb R^n\) formed from the columns of \(P\) (linearly independent eigenvectors of \(A\)), then the \(B\)-matrix of \(\overrightarrow{x} \mapsto A\overrightarrow{x}\) is the diagonal matrix \(D\) whose main diagonal entries are the corresponding eigenvalues of \(A\).


2. The set of all matrix representations (i.e., \(B\)-matrices) of \(\overrightarrow{x} \mapsto A\overrightarrow{x}\) is the set of all matrices similar to \(A\).

Example. \(A=\left[\begin{array}{rr}-1&3\\-3&5\end{array} \right]\). The eigenvalues of \(A\) are \(\lambda=2,2\) with only one linearly independent eigenvector \(\overrightarrow{v}=\left[\begin{array}{r}1\\1\end{array} \right]\). Then \(A\) is not diagonalizable and no \(B\)-matrix of \(\overrightarrow{x} \mapsto A\overrightarrow{x}\) is diagonal. So we find a vector \(\overrightarrow{w}\) such that \((A-\lambda I)^2\overrightarrow{w}=\overrightarrow{0}\) and \((A-\lambda I)\overrightarrow{w}\neq \overrightarrow{0}\). This \(\overrightarrow{w}\) is called a generalized eigenvector of \(A\) corresponding to the eigenvalue \(\lambda=2\). One such \(\overrightarrow{w}\) is \(\overrightarrow{w}=\left[\begin{array}{r}1\\2\end{array} \right]\) which is a generalized eigenvector of \(A\) corresponding to \(\lambda=2\).
Now consider a basis \(B=\left\lbrace \left[\begin{array}{c}1\\1\end{array}\right],\; \left[\begin{array}{c}1\\2\end{array}\right] \right\rbrace\) of \(\mathbb R^2\) consisting of eigenvectors and generalized eigenvectors of \(A\). Then the \(B\)-matrix of \(\overrightarrow{x} \mapsto A\overrightarrow{x}\) is an upper-triangular matrix \[\left[\begin{array}{rr}2&1\\0&2 \end{array} \right]=P^{-1}AP \text{ where } P=\left[\begin{array}{rr}1&1\\1&2\end{array} \right].\] This upper-triangular matrix \(J=P^{-1}AP=\left[\begin{array}{rr}2&1\\0&2 \end{array} \right]\) is called the Jordan form of \(A\).

Theorem. Any \(n\times n\) matrix is similar to an \(n\times n\) matrix in Jordan form, i.e., \(A=PJP^{-1}\) where \(J=\left[\begin{array}{rrr}J_1&&\\ &\ddots&\\ &&J_k \end{array} \right]\), \(J_i=\left[\begin{array}{cccc}\lambda_i&1&&\\ &\lambda_i&\ddots & \\ &&\ddots &1 \\&&&\lambda_i\end{array} \right]\), and \(\lambda_1,\ldots,\lambda_k\) are eigenvalues of \(A\) (not necessarily distinct).

Last edited