LearnMathOnline

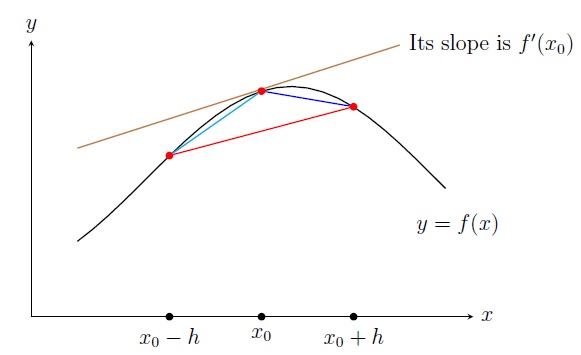
In this section we will numerically find \(f'(x)\) evaluated at \(x=x_0\). We need numerical techniques for derivatives when \(f'(x)\) has a complicated expression or \(f(x)\) is not explicitly given. By the limit definition of derivative, \[f'(x_0)=\lim_{h\to 0}\frac{f(x_0+h)-f(x_0)}{h}.\] So when \(h>0\) is small, we have \[f'(x_0)\approx \frac{f(x_0+h)-f(x_0)}{h},\] which is called the two-point forward difference formula (FDF). Similarly the two-point backward difference formula (BDF) is \[f'(x_0)\approx \frac{f(x_0)-f(x_0-h)}{h}.\] Taking the average of the FDF and BDF, we get the two-point centered difference formula (CDF) is \[f'(x_0)\approx \frac{f(x_0+h)-f(x_0-h)}{2h}.\]

Note that CDF gives better accuracy than FDF and BDF (explained later). But CDF does not work if \(f(x)\) is not known in one side of \(x_0\). All the difference formulas suffer from round-off errors when \(h\) is too small.

Example. \(f(x)=x^2e^{x}\). Approximate \(f'(1)\) using the FDF, BDF, and CDF with \(h=0.2\).

Solution. \[\begin{align*} \text{Two-point FDF}:\; f'(1) &\approx \frac{f(1+0.2)-f(1)}{0.2}=\frac{4.78-2.71}{0.2}=10.35 \\ \text{Two-point BDF}:\; f'(1) &\approx \frac{f(1)-f(1-0.2)}{0.2}=\frac{2.71-1.42}{0.2}=6.45\\ \text{Two-point CDF}:\; f'(1) &\approx \frac{f(1+0.2)-f(1-0.2)}{2(0.2)}= \frac{4.78-1.42}{0.4}=8.4 \end{align*}\] Analytically we know \(f'(1)=3e\). So the absolute errors are \(|10.35-3e|=2.19\), \(|6.45-3e|=1.7\), and \(|8.4-3e|=0.24\) respectively. So CDF gives the least error.

Errors in finite difference formulas: The maximum error in FDF is \[\frac{h}{2} \displaystyle\max_{x\in (x_0,x_0+h)}|f''(x)|.\]

By the Taylor's theorem on \(f\) about \(x_0\), we get \[\begin{align*} f(x)&= f(x_0)+\frac{f'(x_0)}{1!}(x-x_0)+ \frac{f''(\xi)}{2!}(x-x_0)^2. \end{align*}\] Plugging \(x=x_0+h\), we get \[\begin{align*} f(x_0+h)&= f(x_0)+\frac{f'(x_0)}{1!}h+ \frac{f''(\xi_1)}{2!}h^2, \end{align*}\] for some \(\xi_1\in (x_0,x_0+h)\). Solving for \(f'(x_0)\), we get \[f'(x_0)= \frac{f(x_0+h)-f(x_0)}{h}-\frac{f''(\xi_1)}{2}h.\]

So the error in FDF is \(O(h)\) (i.e., absolute error \(\leq ch\) for some \(c>0\)). It means small step size \(h\) results in more accurate derivative. We say FDF is first-order accurate. Similarly BDF is also first-order accurate with the maximum error \[\frac{h}{2} \displaystyle\max_{x\in (x_0-h,x_0)}|f''(x)|.\] The maximum error in CDF is \[\frac{h^2}{6} \displaystyle\max_{x\in (x_0-h,x_0+h)}|f'''(x)|.\] So the error in CDF is \(O(h^2)\), i.e., CDF is second-order accurate which is better than first-order accurate as \(h^2<< h\) for small \(h >0\).

For CDF, note that \[\begin{align*} f(x_0+h)&= f(x_0)+\frac{f'(x_0)}{1!}h+ \frac{f''(x_0)}{2!}h^2+\frac{f'''(\xi_1)}{3!}h^3,\\ f(x_0-h)&= f(x_0)-\frac{f'(x_0)}{1!}h+ \frac{f''(x_0)}{2!}h^2-\frac{f'''(\xi_2)}{3!}h^3, \end{align*}\] for some \(\xi_1\in (x_0,x_0+h)\) and \(\xi_2\in (x_0-h,x_0)\). Subtracting we get, \[\begin{align*} f(x_0+h)-f(x_0-h)&= 2f'(x_0)h+\frac{f'''(\xi_1)+f'''(\xi_2)}{6}h^3\\ \frac{f(x_0+h)-f(x_0-h)}{2h}&= f'(x_0)+\frac{f'''(\xi_1)+f'''(\xi_2)}{12}h^2\\ f'(x_0) &= \frac{f(x_0+h)-f(x_0-h)}{2h}-\frac{f'''(\xi_1)+f'''(\xi_2)}{12}h^2. \end{align*}\] Assuming continuity of \(f'''\) and using the IVT on \(f'''\), we get \[f'''(\xi)=\frac{f'''(\xi_1)+f'''(\xi_2)}{2},\] for some \(\xi\in (\xi_2,\xi_1)\subset (x_0-h,x_0+h)\). Thus \[f'(x_0)= \frac{f(x_0+h)-f(x_0-h)}{2h}-\frac{f'''(\xi)}{6}h^2.\]

Example. Consider \(f(x)=x^2e^{x}\). Find the maximum error in approximating \(f'(1)\) by the FDF, BDF, and CDF with \(h=0.2\).

Solution. \(f''(x)=(x^2+4x+2)e^{x}\) and \(f'''(x)=(x^2+6x+6)e^{x}\) are increasing functions for \(x>0\). So \(\max_{x\in (1,1.2)}|f''(x)|=|f''(1.2)|=27.3\). \[\begin{align*} \text{Maximum error in two-point FDF}:\;&\frac{0.2}{2}\max_{x\in (1,1.2)}|f''(x)|=0.1|f''(1.2)|=2.73 \\ \text{Maximum error in two-point BDF}:\;& \frac{0.2}{2}\max_{x\in (0.8,1)}|f''(x)|=0.1|f''(1)|=1.9\\ \text{Maximum error in two-point CDF}:\;& \frac{(0.2)^2}{6}\max_{x\in (0.8,1.2)}|f'''(x)|=\frac{0.04}{6}|f'''(1.2)|=0.32\\ \end{align*}\]

Derivative from Lagrange polynomial: If \(f\) is not explicitly given but we know \((x_i,f(x_i))\) for \(i=0,1,\ldots,n\), then \(f\) is approximated by the Lagrange polynomial: \[f(x)=\sum_{i=0}^n f(x_i)L_i(x)+\frac{f^{(n+1)}(\xi(x))}{(n+1)!} \prod_{i=0}^n (x-x_i),\] where \(\xi\in (x_0,x_n)\) and \(L_i(x)=\displaystyle\prod_{\substack{j=0\\j\neq i}}^n\frac{(x-x_j)}{(x_i-x_j)}\). Differentiating both sides and evaluating at \(x=x_j\), we get (steps skipped but note that \(\frac{d}{dx} \prod_{i=0}^n (x-x_i)\Big]_{x=x_j}=\prod_{\substack{i=0\\i\neq j}}^n (x_j-x_i)\)) \[f'(x_j)=\sum_{i=0}^n f(x_i)L_i'(x_j)+\frac{f^{(n+1)}(\xi)}{(n+1)!} \prod_{\substack{i=0\\i\neq j}}^n (x_j-x_i).\] If the points \(x_0,x_1,\ldots,x_n\) are equally-spaced, i.e., \(x_j=x_0+jh\), then we get \[f'(x_j)=\sum_{i=0}^n f(x_i)L_i'(x_j)+\frac{f^{(n+1)}(\xi)}{(n+1)!} O(h^n). \] It can be verified that two-point FDF and BDF are obtained from the preceding equation using \(n=1\). Similarly \(n=2\) gives the three-point FDF and BDF and two-point CDF whose errors are \(O(h^2)\): \[\begin{align*} \text{Three-point FDF}:\; f'(x_0) &\approx\frac{-3f(x_0)+4f(x_0+h)-f(x_0+2h)}{2h}\\ \text{Three-point BDF}:\; f'(x_0) &\approx\frac{3f(x_0)-4f(x_0-h)+f(x_0-2h)}{2h} \\ \end{align*}\]

Example. From the following table approximate \(f'(1)\) by the three-point FDF and BDF. \[\begin{array}{|c|c|c|c|c|c|} \hline x & 0.6 & 0.8 & 1 & 1.2 & 1.4\\ \hline f(x) & 0.65 & 1.42 & 2.71 & 4.78 & 7.94\\ \hline \end{array}\] Solution. Here \(h=0.2\). \[\begin{align*} \text{Three-point FDF}:\; f'(1) &\approx\frac{-3f(1)+4f(1+0.2)-f(1+2(0.2))}{2(0.2)}=7.62\\ \text{Three-point BDF}:\; f'(1) &\approx\frac{3f(1)-4f(1-0.2)+f(1-2(0.2))}{2(0.2)} =7.75 \end{align*}\] Note that the table is given for \(f(x)=x^2e^x\). So \(f'(1)=3e\). Then the absolute errors are \(|7.62-3e|=0.53\) and \(|7.75-3e|=0.4\) respectively. Notice that three-point FDF and BDF give less error than two-point FDF and BDF respectively.

Numerical Differentiation