Suppose \(f\) is a function with a unique root \(x^*\) in \([a,b]\). Assume \(f''\) is continuous in \([a,b]\). To find \(x^*\),
let \(x_0\) be a "good" initial approximation (i.e., \(|x^*-x_0|^2 \approx 0\)) where \(f'(x_0)\neq 0\). Using Taylor's Theorem
on \(f\) about \(x_0\), we get
\[f(x)=f(x_0)+\frac{f'(x_0)}{1!}(x-x_0)
+\frac{f''(\xi)}{2!}(x-x_0)^2,\]
for some number \(\xi\) (depends on \(x\)) between \(x_0\) and \(x\). Plugging \(x=x^*\), we get
\[\begin{align*}
& 0=f(x^*)=f(x_0)+\frac{f'(x_0)}{1!}(x^*-x_0)
+\frac{f''(\xi)}{2!}(x^*-x_0)^2\\
\implies & f(x_0)+\frac{f'(x_0)}{1!}(x^*-x_0)
=-\frac{f''(\xi)}{2!}(x^*-x_0)^2 \approx 0 \;\;(\text{since }|x^*-x_0|^2\approx 0)
\end{align*}\]
Now solving for \(x^*\), we get
\[x^*\approx x_0-\frac{f(x_0)}{f'(x_0)}.\]
So \(x_1=x_0-\frac{f(x_0)}{f'(x_0)}\) is an approximation to \(x^*\). Using \(x_1\), similarly we get
\(x_2=x_1-\frac{f(x_1)}{f'(x_1)}\). Continuing the process, we get a sequence \(\{x_n\}\) to approximate \(x^*\) where
\[\boxed{x_{n+1}=x_n-\frac{f(x_n)}{f'(x_n)},\; n=0,1,2,\ldots}\]
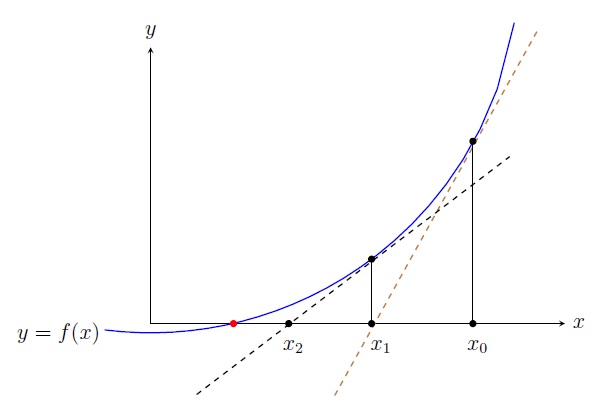
Observation.
\(x_{n+1}\) is the \(x\)-intercept of the tangent line to \(y=f(x)\) at \((x_n,f(x_n))\).
The equation of the tangent line to \(y=f(x)\) at \((x_n,f(x_n))\) is
\[y=f(x_n)+f'(x_n)(x-x_n).\]
For the \(x\)-intercept, \(y=0\). So
\[0=f(x_n)+f'(x_n)(x-x_n)\implies x=x_n-\frac{f(x_n)}{f'(x_n)}.\]
Thus \(x_{n+1}\) is the \(x\)-intercept of the tangent line to \(y=f(x)\) at \((x_n,f(x_n))\).
Remark. We will show later that \(\{x_n\}\) converges to \(x^*\) for a good choice of an initial approximation \(x_0\).
If \(x_0\) is far from \(x^*\), then \(\{x_n\}\) may not converge to \(x^*\). For example, \(f(x)=x^2-5\) has a unique root
\(x^*=\sqrt{5}\) in \([-2,3]\). But the Newton-Raphson Method constructs a sequence \(\{x_n\}\) using \(x_0=-2\)
that converges to \(-\sqrt{5}\neq x^*\).
Example.
Do four iterations by the Newton-Raphson Method to approximate the root \(x^*\) of \(f(x)=e^x-x-2\) on the interval \([0,2]\)
using \(x_0=1\).
Solution. \(f(x)=e^x-x-2 \implies f'(x)=e^x-1\) and \(f'(1)=e-1\neq 0\). Thus
\[x_{n+1}
=x_n-\frac{e^{x_n}-x_n-2}{e^{x_n}-1},\; n=0,1,2,\ldots\]
\[\begin{array}{|l|l|c|l|l|}
\hline n & x_n & f(x_n) & f'(x_n) & x_{n+1}=x_n-\frac{f(x_n)}{f'(x_n)}\\
\hline 0 & 1 & -0.2817 & 1.7182 & 1.1639 \\
\hline 1 & 1.1639 & 0.0384 & 2.2023 & 1.1464 \\
\hline 2 & 1.1464 & 0.0004 & 2.1468 & 1.1462 \\
\hline 3 & 1.1462 & 0.0000 & 2.1462 & 1.1462 \\
\hline
\end{array}\]
Since \(|x_4-x_3|<10^{-4}\), we can say that the root is \(x_4=1.1462\) roughly correct to four decimal places
(almost true as \(x^*=1.146193\)). Actually \(x_4\) is correct to 12 decimal places! Note that this sequence converges
to the root faster than that of other methods (why?).
Convergence: Suppose \(f\) is a function with a simple root \(x^*\) in \([a,b]\), i.e., \(f'(x^*)\neq 0\).
Assume \(f''\) is continuous in \([a,b]\). Then there is a \(\delta>0\) such that the sequence \(\{x_n\}\) constructed by
the Newton-Raphson Method converges to \(x^*\) for any choice of the initial approximation \(x_0\in (x^*-\delta,x^*+\delta)\).
Consider the following function \(g\) on \([a,b]\):
\[g(x)=x-\frac{f(x)}{f'(x)}\]
First note that \(x^*\) is a fixed point of \(g\) in \([a,b]\). Since \(f'(x^*)\neq 0\), by the continuity of \(f'\)
in \([a,b]\), there is a \(\delta_1>0\) such that \(f'(x)\neq 0\) for all \(x\in [x^*-\delta_1,x^*+\delta_1]\).
So \(g\) is continuous on \([x^*-\delta_1,x^*+\delta_1]\).
The convergence follows by that of the Fixed Point Iteration of \(g\) on \([x^*-\delta,x^*+\delta]\) if we can show that there
is a positive \(\delta<\delta_1\) such that
(i) \(x^*-\delta\leq g(x)\leq x^*+\delta\) for all \(x\in [x^*-\delta,x^*+\delta]\) and (ii) \(|g'(x)|<1\) for all
\(x\in(x^*-\delta,x^*+\delta)\). To prove (ii), note that
\[\begin{align*}
& g'(x)=1-\frac{f'(x)f'(x)-f(x)f''(x)}{(f'(x))^2}=\frac{f(x)f''(x)}{(f'(x))^2}\\
\implies & g'(x^*)=\frac{f(x^*)f''(x^*)}{(f'(x^*))^2}=0\;\; (\text{since }f(x^*)=0,\;f'(x^*)\neq 0)
\end{align*}\]
Since \(g'(x^*)=0\), by the continuity of \(g'\) in \([x^*-\delta,x^*+\delta]\), there is a positive \(\delta<\delta_1\)
such that \(|g'(x)|<1\) for all \(x\in (x^*-\delta,x^*+\delta)\). So we have (ii). To show (i), take
\(x\in [x^*-\delta,x^*+\delta]\). By the MVT on \(g\), we have \(g(x)-g(x^*)=g'(\xi)(x-x^*)\) for some \(\xi\) between \(x\)
and \(x^*\). Thus
\[|g(x)-x^*|=|g(x)-g(x^*)|=|g'(\xi)||x-x^*|<|x-x^*|.\]
Since \(x\in [x^*-\delta,x^*+\delta]\), i.e., \(|x-x^*|\leq \delta\), we have \(|g(x)-x^*|<|x-x^*|\leq \delta\), i.e.,
\(x^*-\delta\leq g(x)\leq x^*+\delta\). ◼
Note that if the root \(x^*\) of \(f\) is not simple, i.e., \(f'(x^*)=0\), then this proof does not work but still
\(\{x_n\}\) may converge to \(x^*\). For multiple root \(x^*\) of \(f\) we use a modified Newton-Raphson iteration formula.
The Secant Method: In the iteration formula by the Newton-Raphson Method
\[x_{n+1}=x_n-\frac{f(x_n)}{f'(x_n)},\; n=0,1,2,\ldots,\]
we need to calculate the derivative \(f'(x_n)\) which may be difficult sometimes. To avoid such calculations, the
Secant Method modifies the above formula by replacing \(f'(x_n)\) with its approximation. Note that
\[f'(x_n)=\lim_{x\to x_n}\frac{f(x)-f(x_n)}{x-x_n}.\]
If \(x_{n-1}\) is close to \(x_n\), then
\[f'(x_n)\approx\frac{f(x_{n-1})-f(x_n)}{x_{n-1}-x_n}
=\frac{f(x_n)-f(x_{n-1})}{x_n-x_{n-1}}.\]
Thus
\[x_{n+1}=x_n-\frac{f(x_n)}{f'(x_n)}\approx
x_n-\frac{f(x_n)}{\frac{f(x_n)-f(x_{n-1})}{x_n-x_{n-1}}}=x_n-\frac{(x_n-x_{n-1})f(x_n)}{f(x_n)-f(x_{n-1})}.\]
Thus the iteration formula by the Secant Method is
\[\boxed{x_{n+1}=x_n-\frac{(x_n-x_{n-1})f(x_n)}{f(x_n)-f(x_{n-1})},\; n=1,2,3,\ldots}\]
Note that geometrically \(x_{n+1}\) is the \(x\)-intercept of the secant line joining \((x_n,f(x_n))\) and
\((x_{n-1},f(x_{n-1}))\). Also note that the convergence of the sequence \(\{x_n\}\) by the Secant Method is slower
than that of the Newton-Raphson Method.
