There are some problems in approximating an unknown function \(f\) on \([x_0,x_n]\) by a single polynomial \(P_n\) using \(n+1\) points \((x_0,y_0),\;(x_1,y_1),\ldots,(x_n,y_n)\):
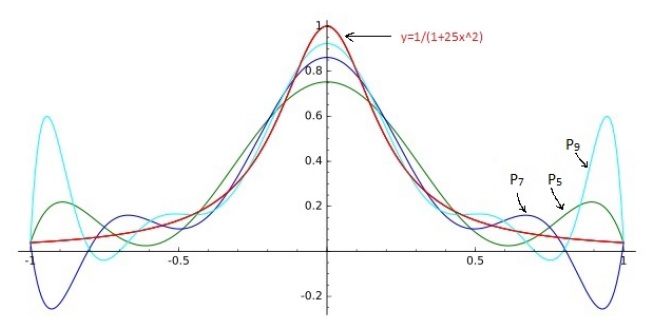
The values \(P_n(x)\) may oscillate near the end points (Runge's phenomenon) and then the maximum error \(|f(x)-P_n(x)|\to \infty\) as \(n\to \infty\), i.e., the error grows for more points. For example, consider the Runge's function \(f(x)=1/(1+25x^2)\) on \([-1,1]\).

To avoid these problems, we use a piecewise interpolating polynomial \(S\) on the intervals \([x_0,x_1]\), \([x_1,x_2]\), \(\ldots,[x_{n-1},x_n]\). This is called piecewise polynomial interpolation. But in the piecewise linear interpolation, the piecewise linear polynomial \(S\) is not smooth i.e., \(S'(x)\) is not continuous at \(x_0,x_1,\ldots,x_n\). If \(S\) is piecewise quadratic, then we get the smoothness but it does not work when \(S'(x_0)\) and \(S'(x_n)\) are given. So we will study piecewise cubic interpolation.

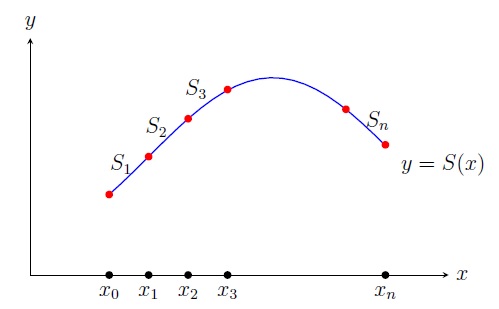
A spline \(S\) of degree \(k\) is a piecewise polynomial of degree at most \(k\) such that \(S^{(k-1)}\) is continuous. A cubic spline is a piecewise cubic with continuous first and second derivatives:

1. \(S(x)=S_i(x)\) on \([x_{i-1},x_i]\) for \(i=1,\ldots,n\),
   
   
2. \(S_i(x_i)=y_i=S_{i+1}(x_i)\) for \(i=1,\ldots,n-1\),
   \(S_1(x_0)=y_0\), and \(S_n(x_n)=y_n\),
   
   
3. \(S_i'(x_i)=S_{i+1}'(x_i)\) for \(i=1,\ldots,n-1\),
   
   
4. \(S_i''(x_i)=S_{i+1}''(x_i)\) for \(i=1,\ldots,n-1\).

A cubic spline \(S\) is called natural if \(S''(x_0)=S''(x_n)=0\) and clamped if \(S'(x_0)\) and \(S'(x_n)\) are provided.

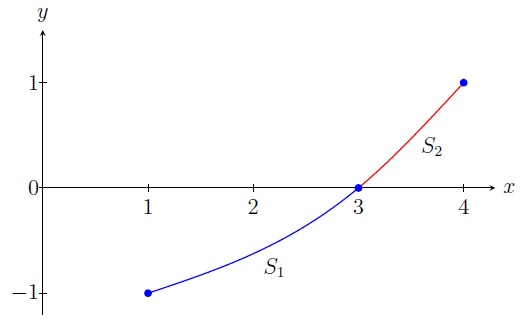
Example. Approximate \(f(2)\) by constructing a natural cubic spline \(S\) from the following data: \[\begin{array}{|r|r|} \hline x & f(x)\\ \hline 1 & -1\\ \hline 3 & 0\\ \hline 4 & 1\\ \hline \end{array}\]
Solution. We define \(S\) piecewise on \([1,4]\) as follows: \[S(x)= \begin{cases} S_1(x)=a_1+b_1(x-1)+c_1(x-1)^2+d_1(x-1)^3 & \text{if } x\in [1,3]\\ S_2(x)=a_2+b_2(x-3)+c_2(x-3)^2+d_2(x-3)^3 & \text{if } x\in [3,4]. \end{cases}\] Using the conditions of cubic spline together with the natural boundary conditions, we get a system of 8 equations in 8 variables: \[\begin{aligned} & S_1(1)=-1 &&\implies a_1=-1\\ & S_1(3)=0 &&\implies a_1+2b_1+4c_1+8d_1=0\\ & S_2(3)=0 &&\implies a_2=0\\ & S_2(4)=1 &&\implies a_2+b_2+c_2+d_2=1\\ & S_1'(3)=S_2'(3) &&\implies b_1+4c_1+12d_1=b_2\\ & S_1''(3)=S_2''(3) &&\implies 2c_1+12d_1=2c_2\\ & S_1''(1)=0 &&\implies 2c_1=0\\ & S_2''(4)=0 &&\implies 2c_2+6d_2=0 \end{aligned}\] Solving (using linear algebra) we get the unique solution \[(a_1,b_1,c_1,d_1,a_2,b_2,c_2,d_2)=\left(-1,\frac{1}{3},0,\frac{1}{24},0,\frac{5}{6},\frac{1}{4},-\frac{1}{12}\right).\] Thus \[S(x)= \begin{cases} -1+ \frac{1}{3}(x-1)+\frac{1}{24}(x-1)^3 & \text{if } x\in [1,3]\\ \frac{5}{6}(x-3)+\frac{1}{4}(x-3)^2-\frac{1}{12}(x-3)^3 & \text{if } x\in [3,4]. \end{cases}\] Thus \(f(2)\approx S(2)=-\frac{15}{24}\).

Note in the preceding example that we got a unique solution and hence a unique natural cubic spline. But we did not just get lucky because this is the case always:

Theorem. There is a unique natural and clamped cubic spline passing through \(n+1\) points \((x_0,y_0),\;(x_1,y_1),\ldots,(x_n,y_n),\; n\geq 2\).

Note that a clamped cubic spine usually gives better approximation than that of a natural cubic spine near the endpoints of \([x_0,x_n]\).

Last edited