You should revise the limit definitions of the derivative and the Riemann integral of a function from a standard text book.
The following are some theorems which will be used later.
Theorem.
Let \(f\) be a differentiable function on \([a,b]\).
- \(f\) is increasing on \([a,b]\) if and only if \(f'(x)>0\) for all \(x\in [a,b]\).
- If \(f\) has a local maximum or minimum value at \(c\), then \(f'(c)=0\) (\(c\) is a critical number).
- If \(f'(c)=0\) and \(f''(c)<0\), then \(f(c)\) is a local maximum value.
- If \(f'(c)=0\) and \(f''(c)>0\), then \(f(c)\) is a local minimum value.
Theorem. Let \(f\) be a continuous function on \([a,b]\). If \(f(c)\) is the absolute maximum or minimum value
of \(f\) on \([a,b]\), then either \(f'(c)\) does not exist or \(f'(c)=0\) or \(c=a\) or \(c=b\).
Intermediate Value Theorem: Let \(f\) be a function such that
- \(f\) is continuous on \([a,b]\), and
- \(N\) is a number between \(f(a)\) and \(f(b)\).
Then there is at least one number \(c\) in \((a,b)\) such that \(f(c)=N\).
In the particular case when \(f(a)f(b)<0\), i.e., \(f(a)\) and \(f(b)\) are of opposite signs, there is at least one root \(c\)
of \(f\) in \((a,b)\).
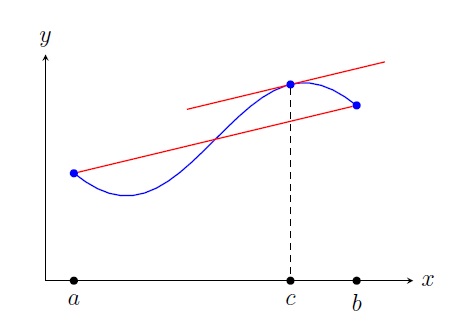
Mean Value Theorem: Let \(f\) be a function such that
- \(f\) is continuous on \([a,b]\), and
- \(f\) is differentiable on \((a,b)\).
Then there is a number \(c\) in \((a,b)\) such that
\[\frac{f(b)-f(a)}{b-a}=f'(c).\]
Taylor's Theorem: Let \(n\geq 1\) be an integer and \(f\) be a function such that
- \(f^{(n)}\) is continuous on \([a,b]\), and
- \(f^{(n)}\) is differentiable on \((a,b)\).
Let \(c\) be a number in \((a,b)\). Then for all \(x\) in \([a,b]\), we have
\[f(x)=f(c)+\frac{f'(c)}{1!}(x-c)+\frac{f''(c)}{2!}(x-c)^2+\cdots
+\frac{f^{(n)}(c)}{n!}(x-c)^n
+\frac{f^{(n+1)}(\xi)}{(n+1)!}(x-c)^{n+1},\]
for some number \(\xi\) (depends on \(x\) ) between \(c\) and \(x\).
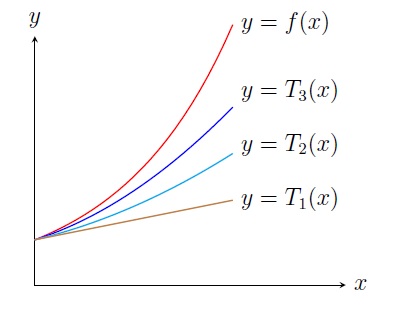
Sometimes we simply write \(f(x)=T_n(x)+R_n(x)\), where \(T_n(x)=\displaystyle\sum_{k=0}^n \frac{f^{(k)}(c)}{k!}(x-c)^k\)
is the Taylor polynomial of degree \(n\) and \(R_n(x)=\displaystyle\frac{f^{(n+1)}(\xi)}{(n+1)!}(x-c)^{n+1}\)
is the remainder term.
Last edited


