A differential equation is an equation containing a function and its derivatives.

Example.

1. \(\displaystyle\frac{dy}{dx}=y\sin x\)


2. \(\displaystyle\frac{dv}{dt}=g-\frac{\gamma}{m}v\) (motion of a falling object)


3. \(\displaystyle\frac{d^2\theta}{dt^2}+\frac{g\sin \theta}{L}=0\) (motion of a pendulum)


4. \(\displaystyle\frac{\partial u}{\partial t}=k\frac{\partial^2u}{\partial x^2}\) (one-dimensional heat equation)

Since derivative of a function means rate of change of the function, many physical phenomenon can be expressed or modelled as differential equations.

Motion of a falling object:
Suppose an object of mass \(m\) is falling under the gravitational force. Suppose \(v\) is its velocity at time \(t\). So its acceleration is \(\displaystyle\frac{dv}{dt}\). If \(F\) is the force exerted on the object at time \(t\), by Newton's second law of motion we have \[\begin{align*} F=m\displaystyle\frac{dv}{dt} && (1) \end{align*}\] Note that two external forces are acting on the object:

1. \(mg\), the weight of the object (\(g\) is the gravitational acceleration which is \(9.8\, m/s^2\))


2. \(D\), the drag or air resistance. It is modelled to be proportional to \(v\). So \(D=\gamma v\) where \(\gamma\) is the drag coefficient which depends on the shape and the velocity of the object and the density of the air.

Thus \(F=mg-\gamma v\). From (1), we have \[\begin{equation*} m\displaystyle\frac{dv}{dt}=mg-\gamma v \end{equation*}\] Dividing both sides by \(m\), we get \[\begin{align*} \displaystyle\frac{dv}{dt}=g-\frac{\gamma}{m} v&& (2) \end{align*}\]

A particular case:
Suppose a particle of mass \(5\) kg is dropped. Suppose the drag coefficient is \(1\,kg/m\). Then (2) becomes the following initial value problem (IVP): \[\begin{equation}\label{eq2} \displaystyle\frac{dv}{dt}=9.8-\frac{v}{5},\; v(0)=0 \end{equation}\] Solve the above differential equation, i.e., find \(v\) as a function of \(t\). \[\begin{align*} \displaystyle\frac{dv}{dt}&=9.8-\frac{v}{5}=\frac{49-v}{5}\\ \displaystyle\frac{dv}{49-v}&=\frac{dt}{5}\\ \displaystyle\int\frac{dv}{v-49}&=\int\frac{dt}{-5}\\ \ln|v-49|&=-\frac{t}{5}+c,\text{ where \(c\) is an integration constant} \\ |v-49|&=e^{c-t/5}=e^ce^{-t/5}\\ v&=49+ke^{-t/5},\text{ where }k=\pm e^c \end{align*}\]

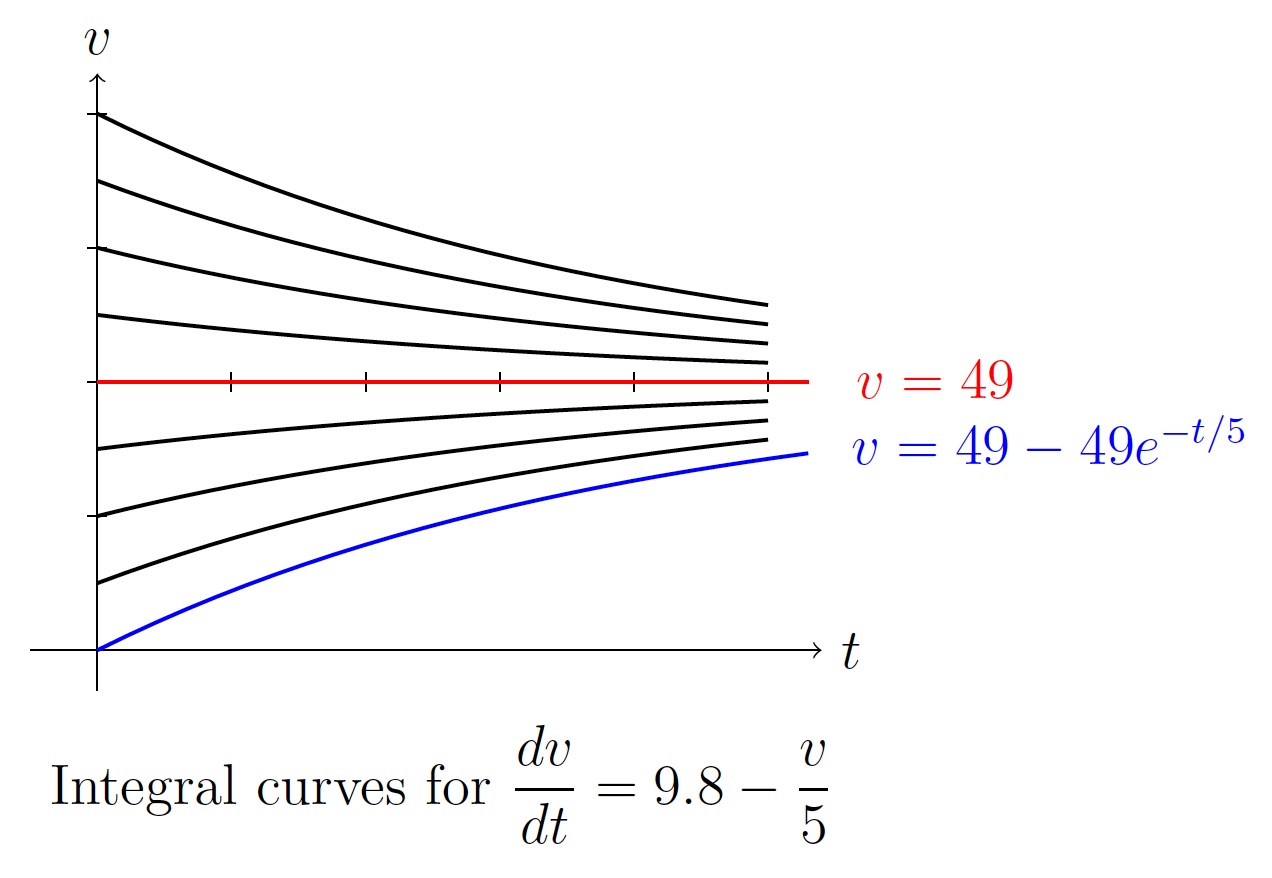
Checking the solution: For \(v=49+ke^{-t/5}\), \[\displaystyle\frac{dv}{dt}=ke^{-t/5}\left(-\frac{1}{5}\right)=(v-49)\left(-\frac{1}{5}\right)=9.8-\frac{v}{5}.\] Note that for each value of \(k\), \(v=49+ke^{-t/5}\) satisfies the following differential equation \[\begin{align*} \displaystyle\frac{dv}{dt}=9.8-\frac{v}{5}&& (3) \end{align*}\] There are infinitely many solutions for differential equation (3). So \(v=49+ke^{-t/5}\) is called the general solution of differential equation (3). Infinitely many solution curves corresponding to the general solution are called integral curves of the general solution. Assigning a particular value of \(k\) in the general solution we get a particular solution to differential equation (3).

We can find a particular value of \(k\) from \(v=49+ke^{-t/5}\) using the initial condition \(v(0)=0\): \[0=49+ke^0 \implies k=-49.\] So \(v=49-49e^{-t/5}\) is the solution of the initial value differential equation (2).

End behavior of \(v\):
Note that as \(t\to \infty\), \(v=49+ke^{-t/5}\to 49\).

Equilibrium Solution and Direction Fields:
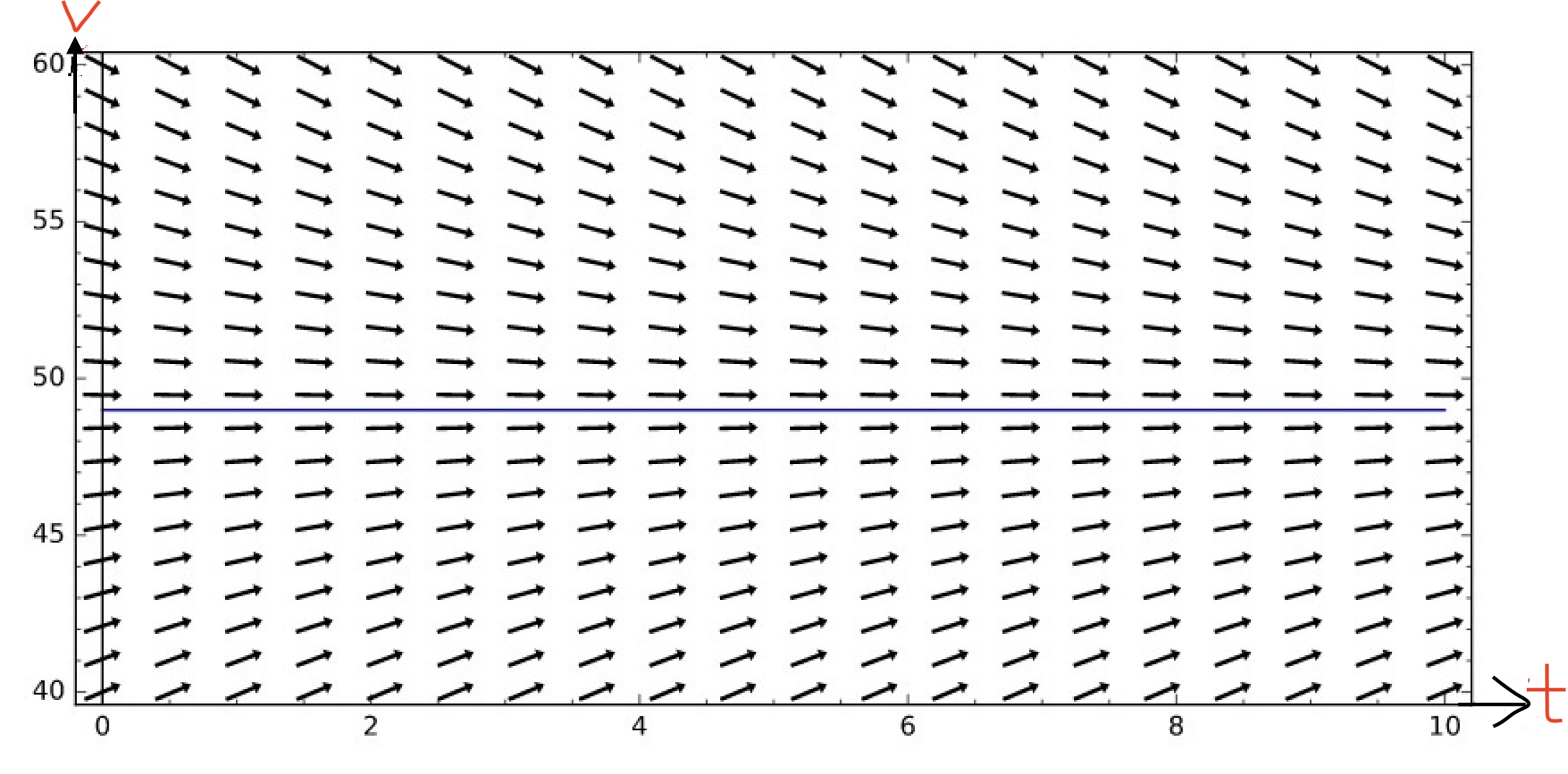
An equilibrium solution is a particular solution to a differential equation that does not change with the independent variable, i.e., the derivative is zero. For the preceding problem, \(v=49\) is an equilibrium solution. \[\frac{dv}{dt}=9.8-\frac{v}{5}=0\implies v=49.\] Clearly \(\frac{dv}{dt}=9.8-\frac{v}{5} > 0\) when \(v< 49\) and \(\frac{dv}{dt}=9.8-\frac{v}{5} < 0\) when \(v > 49\).

In the \(t-v\) graph, for a given value of \(v\), we draw a vector with the slope \(\frac{dv}{dt}\). For example, for \(v=49\), we have \(\frac{dv}{dt}=0\) and we get horizontal vectors on the line \(v=49\). For \(v=45\), we have \(\frac{dv}{dt}=0.8\) and we get vectors with slope \(0.8\) on the line \(v=45\). This vector plotting on the \(tv\)-plane gives the direction field} or slope field of differential equation (3).

Last edited