Motion of a simple pendulum:
Consider a "simple'' pendulum with length \(L\). Let \(\theta(t)\) be its angular displacement at time \(t\). By Newton's second law (i.e., mass \(\cdot\) acceleration= net force) we get \[\begin{align*} &\frac{d^2\theta}{dt^2}=-\frac{g}{L}\sin \theta\\ \text{i.e., }&\frac{d^2\theta}{dt^2}+\frac{g}{L}\sin \theta =0. \end{align*}\] This nonlinear ODE has no solution in terms of usual functions. So it is linearized by taking \(\sin \theta\approx \theta\) for \(\theta\approx 0\): \[\frac{d^2\theta}{dt^2}+\frac{g}{L} \theta =0.\] The characteristic equation is \[r^2+\frac{g}{L}=0 \implies r=\pm i\sqrt{\frac{g}{L}}.\] The general solution is \[\theta=c_1\cos\left(\sqrt{\frac{g}{L}}t \right)+c_2\sin\left(\sqrt{\frac{g}{L}}t \right).\] Using the initial conditions \(\theta(0)=\theta_0\) and \(\theta'(0)=0\), we get \(c_1=\theta_0\) and \(c_2=0\). Thus \[\theta=\theta_0\cos\left(\sqrt{\frac{g}{L}}t \right).\]

Kirchhoff's voltage law:
Consider an electric circuit with a resistor, an inductor, a capacitor, and a battery arranged in series (RLC circuit). Let \(Q(t)\) be the charge of the capacitor and \(I(t)\) current at time \(t\). Then Kirchhoff's voltage law states that the sum of the voltage drops across the resistor, inductor, and capacitor is equal to the supplied voltage \(V(t)\): \[L\frac{dI}{dt}+RI+\frac{Q}{C}=V,\] where \(L\) is the constant inductance, \(R\) is the constant resistant and \(C\) is the constant capacitance. Since \(I\) is the rate of change of \(Q\) with respect to time \(t\), \(I=\frac{dQ}{dt}\). Then the preceding ODE becomes \[L\frac{d^2Q}{dt^2}+R\frac{dQ}{dt}+\frac{Q}{C}=V.\]

Vibrating springs:
Consider a horizontal or a vertical spring with one end attached to a firm base and the other end an object of mass \(m\). If the spring is stretched or compresses \(x\) units from its equilibrium position, it exerts a restoring force \(F_r\) which is proportional to \(x\) by Hooke's Law: \[F_r=-kx,\] where \(k > 0\) is the spring constant. Ignoring other forces like friction, by Newton's Second Law we get \[m\frac{d^2x}{dt^2}= F_r \implies m\frac{d^2x}{dt^2}=-kx \implies m\frac{d^2x}{dt^2}+kx=0.\] The characteristic equation is \(mr^2+k=0\implies r=\pm i\sqrt{k/m}\). So the general solution is \[x=c_1\cos(\sqrt{k/m} t)+c_2\sin(\sqrt{k/m} t)=A\cos(\omega t+\delta),\] where \(A=\sqrt{c_1^2+c_2^2}\), \(\omega=\sqrt{k/m}\), and \(\delta=\tan^{-1}(c_2/c_1)\) are the amplitude, frequency, and phase angle respectively. This is an example of simple harmonic motion.

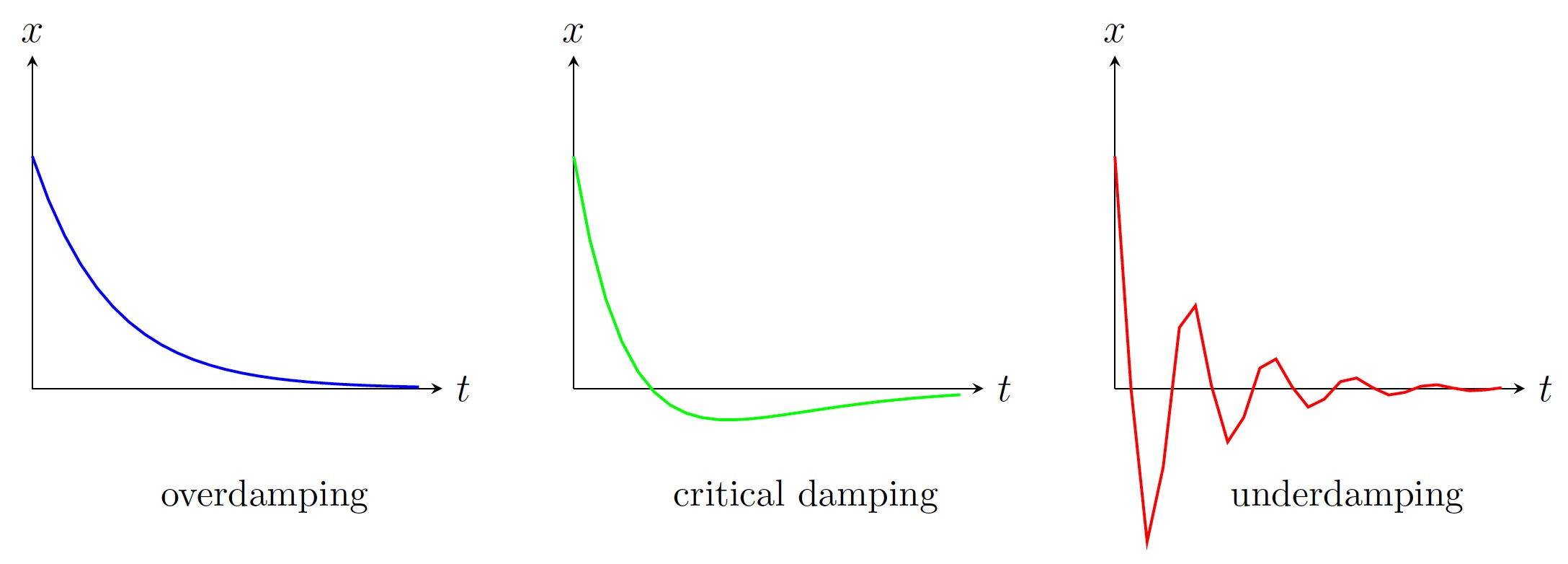
Damped vibrations:
Consider a horizontal spring with friction of the surface or a vertical spring with a damping force of the medium. The damping force \(F_d\) is modeled to be proportional to the velocity, i.e., \[F_d=-c\frac{dx}{dt},\] where \(c > 0\) is the damping constant. By Newton's Second Law we get \[m\frac{d^2x}{dt^2}= F_r+F_d \implies m\frac{d^2x}{dt^2}=-kx-c\frac{dx}{dt} \implies m\frac{d^2x}{dt^2}+c\frac{dx}{dt}+kx=0.\] The characteristic equation is \(mr^2+cr+k=0\implies r_1,r_2=(-c\pm \sqrt{c^2-4mk})/2m\).

1. \(c^2-4mk > 0\) (overdamping): Roots are distinct real negative and \(x=c_1e^{r_1t}+c_2e^{r_2t}\). Here \(c > 2\sqrt{mk}\) implies a high damping force resulting in no vibration.


2. \(c^2-4mk=0\) (critical damping): \(r_1=r_2=-c/2m\) and \(x=(c_1+c_2t)e^{-ct/2m}\). Here \(c=2\sqrt{mk}\) implies the least damping force that suppresses too much vibrations.


3. \(c^2-4mk < 0\) (underdamping): Roots are complex conjugates and \(x=e^{-ct/2m}(c_1\cos(\omega t)+c_2\sin(\omega t))\), \(\omega=\sqrt{4mk-c^2}/2m\). Here \(c < 2\sqrt{mk}\) implies a low damping force failing to suppress too much vibrations.

Last edited