We ask two questions for the following ODE \[\displaystyle\frac{dy}{dx}=f(x,y),\, y(x_0)=y_0 \;\;\;\;(21)\]

1. Is there any solution to (21)? (existence of solution?)


2. Is there a unique solution to (21)? (uniqueness of solution?)

The answers are given by the Existence and Uniqueness Theorem:
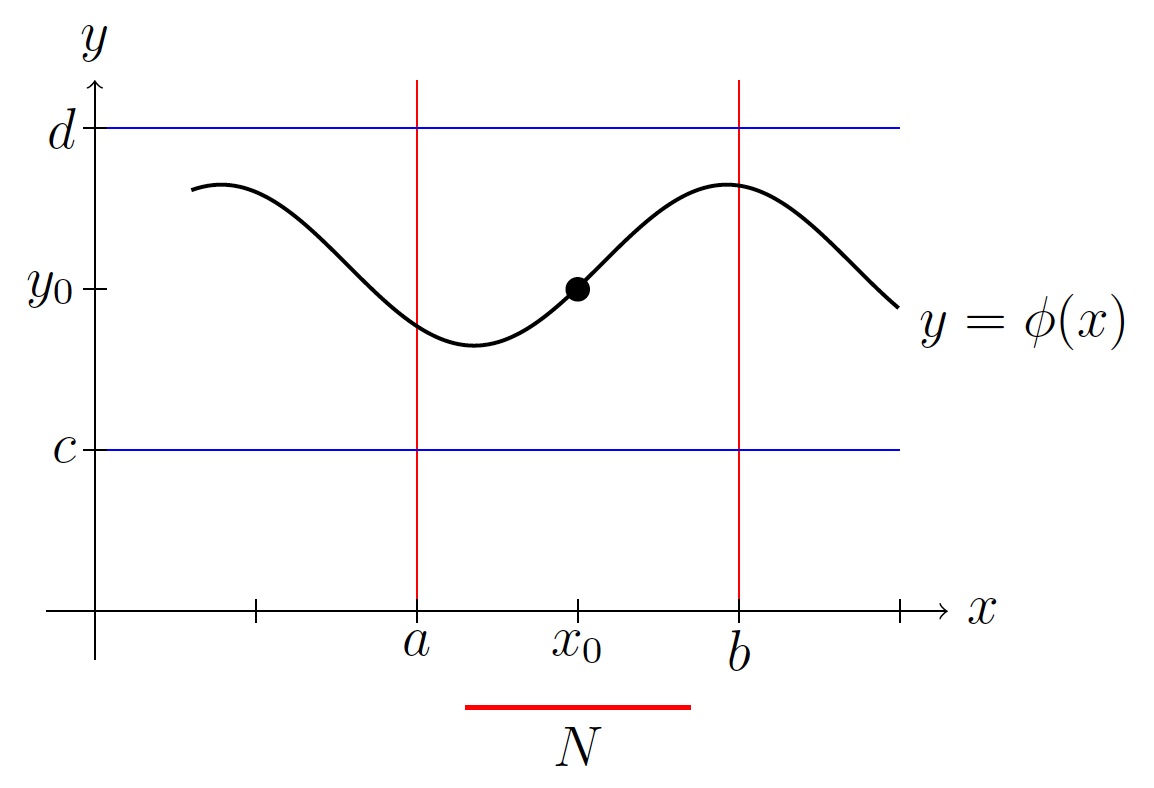
Theorem.

1. If \(f\) is a continuous function on a neighborhood \((a,b)\times (c,d)\) of \((x_0,y_0)\), then there is a solution \(y=\phi(x)\) to (21) in a neighborhood \(N\) of \(x_0\) where \(N\) is inside \((a,b)\).


2. If \(f\) and \(\displaystyle\frac{\partial f}{\partial y}\) are continuous functions on a neighborhood \((a,b)\times (c,d)\) of \((x_0,y_0)\), then there is a unique solution \(y=\phi(x)\) to (21) in a neighborhood \(N\) of \(x_0\) where \(N\) is inside \((a,b)\).

Example. \[y'=\frac{2y}{x},\, y(1)=3\]

1. Determine if the above ODE has a solution.


2. Find the largest interval in which the following ODE has a unique solution.

Solution. (a) Since \(f(x,y)=\displaystyle\frac{2y}{x}\) is continuous function for all values of \((x,y)\) where \(x\neq 0\), the give ODE has a solution \(y=\phi(x)\) in any neighborhood of \(1\) not containing \(0\).

(b) \(f(x,y)=\displaystyle\frac{2y}{x}\) and \(\displaystyle\frac{\partial f}{\partial y}=\displaystyle\frac{2}{x}\) are continuous functions for all values of \((x,y)\) where \(x\neq 0\). Because of the initial condition \(y(1)=3\), the given ODE has a unique solution \(y=\phi(x)\) in the interval \((0,\infty)\) (which is the largest possible neighborhood of \(1\) for \(y=\phi(x)\)).

Remark.

1. If the initial condition were \(y(-1)=3\), then the largest interval would be \((-\infty,0)\) for the unique solution \(y=\phi(x)\).


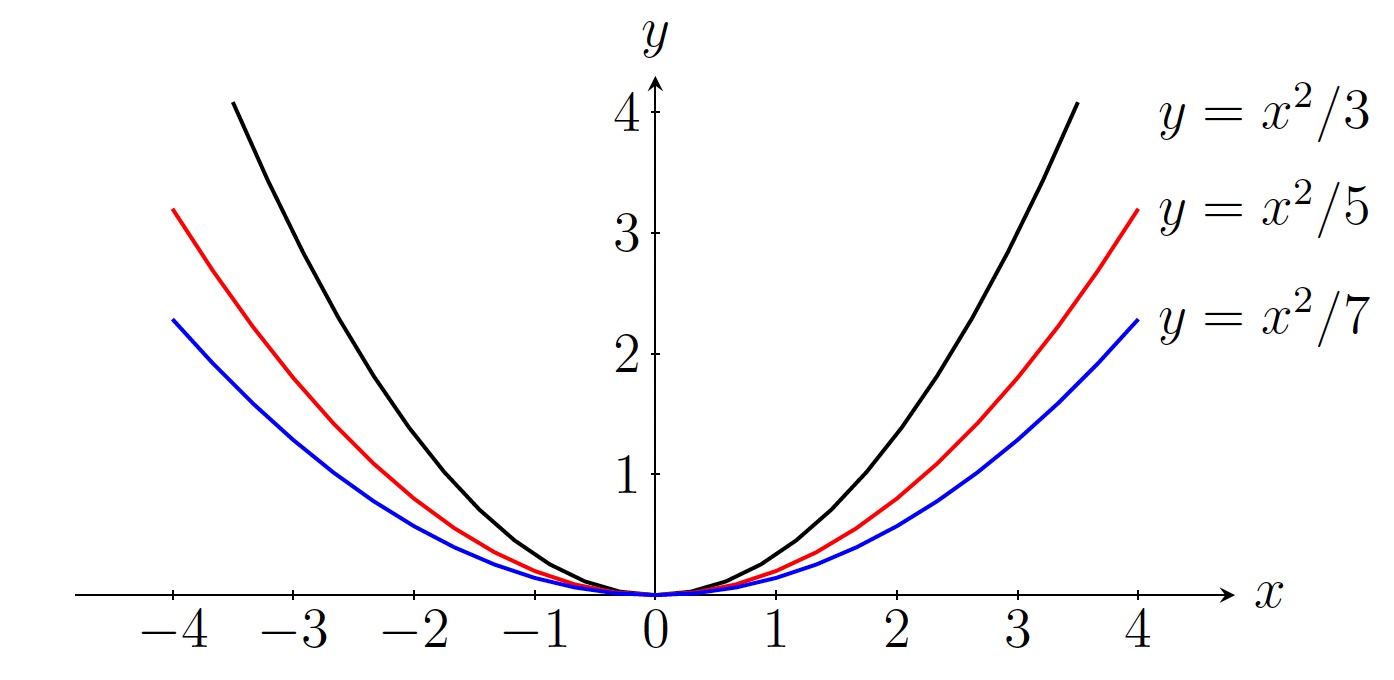
2. Solving the ODE \(y'=\frac{2y}{x}\), we get \(y=cx^2\). So \(y=cx^2\) is a solution of \(y'=\frac{2y}{x}\) for each value of \(c\).


1. If the initial condition were \(y(0)=3\), then there is no solution which makes sense because \(f(x,y)=\displaystyle\frac{2y}{x}\) is not continuous at \((0,3)\).


2. If the initial condition were \(y(0)=0\), then there is infinitely many solutions of the form \(y=cx^2\). It is justified because \(f(x,y)=\displaystyle\frac{2y}{x}\) and \(\displaystyle\frac{\partial f}{\partial y}=\displaystyle\frac{2}{x}\) are not continuous at \((0,0)\).


3. If the initial condition were \(y(x_0)=y_0\) where \(x_0\neq 0\), then there is a unique solution \(y=\frac{y_0}{x_0^2}x^2\). It is justified because \(f(x,y)=\displaystyle\frac{2y}{x}\) and \(\displaystyle\frac{\partial f}{\partial y}=\displaystyle\frac{2}{x}\) are continuous at and near \((x_0,y_0)\) where \(x_0\neq 0\).

Example. Find the largest interval in which the following ODE has a unique solution. Justify your answer. \[(t-1)(t-3)y'-2y=0,\, y(2)=-5\] Solution. \[y'=\frac{2y}{(t-1)(t-3)},\, y(2)=-5\] \(f(t,y)=\displaystyle\frac{2y}{(t-1)(t-3)}\) and \(\displaystyle\frac{\partial f}{\partial y}=\displaystyle\frac{2}{(t-1)(t-3)}\) are continuous functions for all values of \((t,y)\) where \(t\neq 1,3\). Because of the initial condition \(y(2)=-5\), the given ODE has a unique solution \(y=\phi(t)\) in the interval \((1,3)\) (which is the largest possible neighborhood of \(2\) for \(y=\phi(t)\)).

Last edited