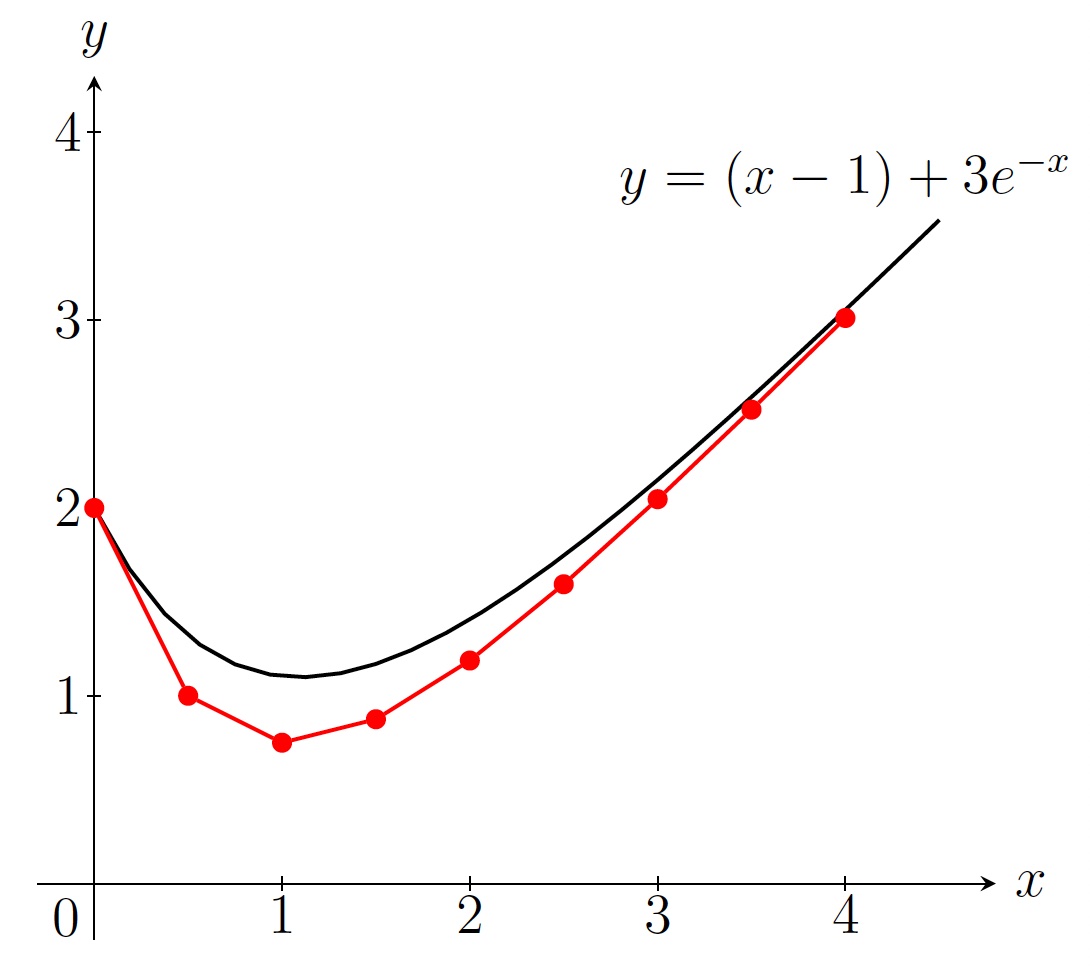
Euler's tangent line approximation to \(\frac{dy}{dx}=x-y,\, y(0)=2\) with \(h=0.5\)
Euler's Method |
Can we numerically find an approximate solution to the following ODE?
\[\displaystyle\frac{dy}{dx}=f(x,y),\, y(x_0)=y_0\]
Euler's Method: The tangent line to a solution \(y=\phi(x)\) at the point \((x_0,y_0)\) has slope
\(\displaystyle\left.\frac{dy}{dx}\right]_{(x_0,y_0)}=f(x_0,y_0)\). So an equation of the tangent line would be
\[y=y_0+(x-x_0)f(x_0,y_0).\]
If \(x_1\) is close to \(x_0\), then \(y_1=y_0+(x_1-x_0)f(x_0,y_0)\) would be a good approximation to \(y=\phi(x_1)\). Similarly if \(x_2\) is close to \(x_1\), then \(y_2=y_1+(x_2-x_1)f(x_1,y_1)\) would be a good approximation to \(y=\phi(x_2)\). Thus a general formula for this tangent line expression would be
\[y_{n+1}=y_n+(x_{n+1}-x_n)f(x_n,y_n),\, n=0,1,2,\ldots.\;\;\;\;(22)\]
If we take \(x_0,x_1,x_3,\ldots\) with a fixed difference \(h\) (i.e. \(x_{n+1}=x_n+h\)), then (22) becomes
\[y_{n+1}=y_n+hf(x_n,y_n),\, n=0,1,2,\ldots.\;\;\;\;(23)\]
Example.
Use Euler's method with step size \(h=0.5\) to approximate \(y(4)\) where \(y=\phi(x)\) is a solution to the following ODE.
\[\frac{dy}{dx}=x-y,\, y(0)=2\]
Solution. We have \(h=0.5,\, x_0=0,\, y_0=2\) and \(f(x,y)=x-y\). So from (23) we have
\(y_{n+1}=y_n+0.5(x_n-y_n),\, n=0,1,2,\ldots.\)
\[\begin{align*}
x_1&=x_0+0.5=0.5, &&y_1=y_0+0.5(x_0-y_0)=2+0.5(0-2)=1\\
x_2&=x_1+0.5=1, &&y_2=y_1+0.5(x_1-y_1)=1+0.5(0.5-1)=0.75\; etc.
\end{align*}\]
\[\begin{array}{|c|l|l|}
\hline n& x_n & y_n \\
\hline 0&0 &2\\
\hline 1&0.5 &1\\
\hline 2&1 &0.75\\
\hline 3&1.5 &0.875\\
\hline 4&2 &1.1875\\
\hline 5&2.5 &1.59375\\
\hline 6&3 &2.046875\\
\hline 7&3.5 &2.5234375\\
\hline 8&4 &3.01171875\\ \hline
\end{array}\]
So \(y(4) \approx y_8=3.01171875\), i.e., \(y(4)\) is approximately \(y_8=3.01171875\).

Euler's tangent line approximation to \(\frac{dy}{dx}=x-y,\, y(0)=2\) with \(h=0.5\)
Checking solution: Solving \(\displaystyle\frac{dy}{dx}=x-y,\, y(0)=2\), we get \(y=(x-1)+3e^{-x}\). The exact value of \(y(4)\) is \((4-1)+3e^{-4}=3.0183\) which was approximated by \(3.0117\). (pretty close!)
Last edited