A power series is a series of the form \[ \sum_{n=0}^{\infty} a_n x^n=a_0+a_1x+a_2x^2+a_3x^3+\cdots. \] A power series about \(c \) (or, centered at \(c \)) is a series of the form \[ \sum_{n=0}^{\infty} a_n (x-c)^n=a_0+a_1(x-c)+a_2(x-c)^2+a_3(x-c)^3+\cdots. \]

Example.

1. \(\displaystyle\sum_{n=0}^{\infty} x^n=1+x+x^2+x^3+\cdots \) is a power series about \(0 \).
2. \(\displaystyle\sum_{n=0}^{\infty} \frac{(x-2)^n}{n!}=1+\frac{(x-2)}{1!}+\frac{(x-2)^2}{2!}+\frac{(x-2)^3}{3!}+\cdots\) is a power series about \(2\).

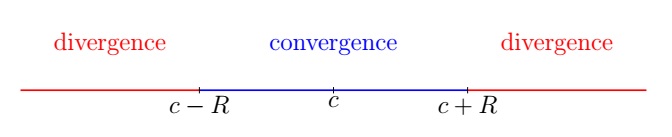
Theorem. There are three possibilities regarding convergence of a power series \(\displaystyle\sum_{n=0}^{\infty} a_n (x-c)^n\):

1. \(\displaystyle\sum_{n=0}^{\infty} a_n (x-c)^n\) converges only for \(x=c\).
   
2. \(\displaystyle\sum_{n=0}^{\infty} a_n (x-c)^n\) converges for all values of \(x\).
   
3. There is a positive real number \(R\) such that \(\displaystyle\sum_{n=0}^{\infty} a_n (x-c)^n\) converges if \(|x-c| < R\) and diverges if \(|x-c| > R\).
   

Example. The power series \(\displaystyle\sum_{n=0}^{\infty} x^n=1+x+x^2+x^3+\cdots\) is a geometric series with the common ratio \(x\). Therefore it converges if \(|x| < 1\) and diverges if \(|x|\geq 1\). So in this case, \(R=1\).

Definition. If \(\displaystyle\sum_{n=0}^{\infty} a_n (x-c)^n\) converges for \(|x-c| < R\) and diverges for \(|x-c| > R\), then \(R\) is called the radius of convergence of \(\displaystyle\sum_{n=0}^{\infty} a_n (x-c)^n\). We define \(R\) to be \(0\) or \(\infty\) if \(\displaystyle\sum_{n=0}^{\infty} a_n (x-c)^n\) converges only for \(x=c\) and for all values of \(x\) respectively. The interval of convergence of \(\displaystyle\sum_{n=0}^{\infty} a_n (x-c)^n\) is the interval that contains all the values of \(x\) for which \(\displaystyle\sum_{n=0}^{\infty} a_n (x-c)^n\) converges.

Note that the interval of convergence contains \((c-R,c+R)\).

Example. Find the radius of convergence and the interval of convergence of the power series \[\displaystyle\sum_{n=1}^{\infty} \frac{(2x-1)^n}{3^n\sqrt{n}}.\]
Solution. Here \[a_n=\frac{(2x-1)^n}{3^n\sqrt{n}}=\frac{2^n \left(x-\frac{1}{2}\right)^n}{3^n\sqrt{n}}=\left(\frac{2}{3}\right)^n \frac{\left(x-\frac{1}{2}\right)^n}{\sqrt{n}}.\] Then \[a_{n+1}=\left(\frac{2}{3}\right)^{n+1} \frac{\left(x-\frac{1}{2}\right)^{n+1}}{\sqrt{n+1}}\] and \[ \frac{a_{n+1}}{a_n}=\left(\frac{2}{3}\right)^{n+1} \frac{\left(x-\frac{1}{2}\right)^{n+1}}{\sqrt{n+1}} \left(\frac{3}{2}\right)^n \frac{\sqrt{n}}{\left(x-\frac{1}{2}\right)^n} =\frac{2}{3} \left(x-\frac{1}{2}\right) \sqrt{\frac{n}{n+1}}. \] \[ \lim_{n\to \infty} \left\vert \frac{a_{n+1}}{a_n} \right\vert =\lim_{n\to \infty} \left\vert \frac{2}{3} \left(x-\frac{1}{2}\right) \sqrt{\frac{n}{n+1}} \right\vert =\lim_{n\to \infty} \frac{2}{3} \left\vert x-\frac{1}{2} \right\vert \sqrt{\frac{1}{1+\frac{1}{n}}} =\frac{2}{3} \left\vert x-\frac{1}{2} \right\vert. \] By the Ratio Test, the given power series is convergent if \(\frac{2}{3} \left\vert x-\frac{1}{2} \right\vert < 1\), i.e., \(\left\vert x-\frac{1}{2} \right\vert< \frac{3}{2}\) and divergent if \(\frac{2}{3} \left\vert x-\frac{1}{2} \right\vert > 1\), i.e., \(\left\vert x-\frac{1}{2} \right\vert > \frac{3}{2}\). Thus the radius of convergence is \(R=\frac{3}{2}\).

Since \(\left\vert x-\frac{1}{2} \right\vert < \frac{3}{2} \implies \frac{1}{2}-\frac{3}{2} < x < \frac{1}{2}+\frac{3}{2} \implies -1 < x < 2\), the interval of convergence contains \((-1,2)\). Now we need to determine the convergence for \(x=-1,2\) (the endpoints).

At \(x=2\), the power series becomes \(\displaystyle\sum_{n=1}^{\infty} \frac{(2\cdot 2-1)^n}{3^n\sqrt{n}}= \sum_{n=1}^{\infty} \frac{1}{\sqrt{n}}\) which is divergent by the \(p\)-series Test with \(p=\frac{1}{2}\leq 1\).

At \(x=-1\), the power series becomes \(\displaystyle\sum_{n=1}^{\infty} \frac{(2(-1)-1)^n}{3^n\sqrt{n}}= \sum_{n=1}^{\infty} \frac{(-1)^n}{\sqrt{n}}\). Let \(a_n=\frac{1}{\sqrt{n}}\). For all integers \(n\geq 1\), \(a_n=\frac{1}{\sqrt{n}} > 0\) and \(a_{n+1}=\frac{1}{\sqrt{n+1}} < \frac{1}{\sqrt{n}}=a_n\). Also \(\displaystyle\lim_{n\to \infty} a_n =\lim_{n\to \infty}\frac{1}{\sqrt{n}}=0\). Thus \(\{a_n\}=\{\frac{1}{\sqrt{n}}\}\) is a positive and decreasing sequence that converges to \(0\). By the Alternating Series Test, \(\displaystyle \sum_{n=1}^{\infty} \frac{(-1)^n}{\sqrt{n}}\) is convergent.

Since the power series is convergent at \(-1\) and divergent at \(2\), the interval of convergence is \([-1,2)\).

Definition. Let \(I\) be the interval of convergence of \(\displaystyle\sum_{n=0}^{\infty} a_n (x-c)^n\). The sum function \(f\) of the series is a function with domain \(I\) that is defined as \[f(x)=\sum_{n=0}^{\infty} a_n (x-c)^n,\] for all \(x\) in \(I\).

Example. The power series \(\displaystyle\sum_{n=0}^{\infty} x^n=1+x+x^2+x^3+\cdots\) converges to \(\frac{1}{1-x}\) if \(|x| < 1\) and diverges if \(|x|\geq 1\). So the sum function is \(f(x)=\frac{1}{1-x}\) for all \(x\) in \(I=(-1,1)\) and we write \[\frac{1}{1-x}=\sum_{n=0}^{\infty} x^n=1+x+x^2+x^3+\cdots,\; |x| < 1.\]

The above example helps us write some functions as power series as illustrated by the following example.

Example. Find a power series representation of \(\displaystyle\frac{2x}{x^2+9}\) and its interval of convergence.
Solution. \[\begin{align*} \frac{2x}{x^2+9}=\frac{2x}{9\left( 1+\frac{x^2}{9} \right)}=\frac{2x}{9} \frac{1}{\left( 1-\left(-\frac{x^2}{9}\right) \right)} &=\frac{2x}{9} \sum_{n=0}^{\infty} \left(-\frac{x^2}{9}\right)^n,\; \left\vert -\frac{x^2}{9}\right\vert <1\\ &=\frac{2x}{9} \sum_{n=0}^{\infty} \frac{(-1)^nx^{2n}}{9^n},\; |x^2| <9\\ &=\sum_{n=0}^{\infty} \frac{(-1)^n2x^{2n+1}}{9^{n+1}},\; |x| <3. \end{align*}\] Since the power series converges if and only if \(|x| < 3\), the interval of convergence is \((-3,3)\).

Theorem. Suppose that the power series \(f(x)=\displaystyle\sum_{n=0}^{\infty} a_n (x-c)^n\) has radius of convergence \(R\). Then the power series is differentiable and integrable on \((c-R,c+R)\). Moreover, the power series can be differentiated and integrated term by term: \[\begin{align*} f'(x) &=\displaystyle\sum_{n=1}^{\infty} na_n (x-c)^{n-1}=a_1+2a_2(x-c)+3a_3(x-c)^2+\cdots.\\ \int f(x)\;dx &= C+\displaystyle\sum_{n=0}^{\infty} a_n \frac{(x-c)^{n+1}}{n+1}=C+a_0(x-c)+a_1\frac{(x-c)^2}{2}+a_2\frac{(x-c)^3}{3}+\cdots. \end{align*}\]

The above can alternatively be written as follows: \[\begin{align*} \frac{d}{dx} \left[ \sum_{n=0}^{\infty} a_n (x-c)^n \right] &=\sum_{n=0}^{\infty} \left[ \frac{d}{dx} a_n (x-c)^n \right].\\ \int \left[ \sum_{n=0}^{\infty} a_n (x-c)^n \right]dx &= \sum_{n=0}^{\infty} \left[ \int a_n (x-c)^n \;dx \right]. \end{align*}\]

The preceding theorem can be used to find power series representations of some functions.

Example. Find a power series representation of each of the following functions: (a) \(\ln(1+x)\), (b) \(\frac{1}{(1-x)^2}\).

Solution. (a) Since \(\displaystyle\int \frac{1}{1+x}\;dx=\ln(1+x)\) and \[\frac{1}{1+x}=\frac{1}{1-(-x)}=\sum_{n=0}^{\infty} (-x)^n=\sum_{n=0}^{\infty} (-1)^nx^n,\; |x| < 1,\] we have \[\begin{align*} \ln(1+x) &=\int\frac{1}{1+x} \;dx \\ &= \int \left[ \sum_{n=0}^{\infty} (-1)^nx^n \right] \;dx\\ &= \sum_{n=0}^{\infty} \left[ \int(-1)^nx^n \;dx\right] \\ &= C+\sum_{n=0}^{\infty} (-1)^n \frac{x^{n+1}}{n+1}. \end{align*}\] To find \(C\), we plug \(x=0\): \[ \ln(1)=C+\sum_{n=0}^{\infty} (-1)^n \frac{0^{n+1}}{n+1} \implies C=0.\] Thus \[\ln(1+x)=\sum_{n=0}^{\infty} (-1)^n \frac{x^{n+1}}{n+1}=x-\frac{x^2}{2}+\frac{x^3}{3}-\frac{x^4}{4}+\cdots,\; |x| < 1.\]

(b) Since \(\displaystyle\frac{d}{dx} \left(\frac{1}{1-x} \right)=\frac{1}{(1-x)^2}\) and \[\frac{1}{1-x}=\sum_{n=0}^{\infty} x^n,\; |x|<1,\] we have \[\begin{align*} \frac{1}{(1-x)^2} &= \frac{d}{dx} \left(\frac{1}{1-x} \right)\\ &= \frac{d}{dx} \left[ \sum_{n=0}^{\infty} x^n \right]\\ &= \sum_{n=0}^{\infty} \left[ \frac{d}{dx} (x^n) \right]\\ &= \sum_{n=1}^{\infty} nx^{n-1},\; |x|<1. \end{align*}\]

Last edited