A system of linear equations with \(n\) variables \(x_1,\ldots,x_n\) and \(m\) equations can be written as follows: \[\begin{eqnarray} \begin{array}{ccccccccc} a_{11}x_1&+&a_{12}x_2&+&\cdots &+&a_{1n}x_n&=&b_1\\ a_{21}x_1&+&a_{22}x_2&+&\cdots &+&a_{2n}x_n&=&b_2\\ \vdots&&\vdots&& &&\vdots&&\vdots \tag{1}\\ a_{m1}x_1&+&a_{m2}x_2&+&\cdots &+&a_{mn}x_n&=&b_m. \end{array} \end{eqnarray}\] A solution is an \(n\)-tuple \((s_1,s_2,\ldots,s_n)\) that satisfies each equation when we substitute \(x_1=s_1,x_2=s_2,\ldots,x_n=s_n\). The solution set is the set of all solutions.

Example. \[\begin{eqnarray*} \begin{array}{rcrcrcr} x_1&& &+&x_3&=&3\\ &&x_2&-&2x_3&=&-1 \end{array} \end{eqnarray*}\] The solution set (on \(\mathbb R\)) is \(\{(-s+3,2s-1,s)\; |\; s\in \mathbb R\}\). There are infinitely many solutions because of the free variable \(x_3\).

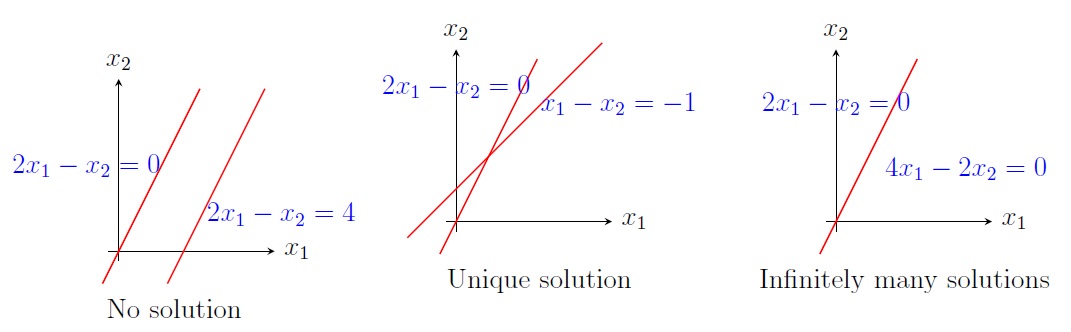
Possibilities of solutions of a linear system:

• System has no solution (Inconsistent)


• System has a solution (Consistent)


• Unique solution


• Infinitely many solutions

Definition. The system (1) is called an underdetermined system if \(m < n\), i.e., fewer equations than variables. The system (1) is called an overdetermined system if \(m > n\), i.e., more equations than variables.

The system (1) of linear equations can be written by a matrix equation and a vector equation:
The matrix equation: \(A\overrightarrow{x}=\overrightarrow{b}\), where \[A=\left[\begin{array}{cccc} a_{11}&a_{12}&\cdots &a_{1n}\\ a_{21}&a_{22}&\cdots &a_{2n}\\ \vdots&\vdots&\ddots &\vdots\\ a_{m1}&a_{m2}&\cdots &a_{mn} \end{array}\right],\; \overrightarrow{x}=\left[\begin{array}{c}x_1\\x_2\\ \vdots\\x_n \end{array} \right], \mbox{ and } \overrightarrow{b}=\left[\begin{array}{c} b_1\\b_2\\ \vdots\\b_m \end{array} \right].\] \(A\) is the coefficient matrix. The augmented matrix is \[[A\:\overrightarrow{b}]=\left[\begin{array}{ccccc} a_{11}&a_{12}&\cdots &a_{1n}&b_1\\ a_{21}&a_{22}&\cdots &a_{2n}&b_2\\ \vdots&\vdots&\ddots &\vdots&\vdots\\ a_{m1}&a_{m2}&\cdots &a_{mn}&b_m \end{array}\right].\] The vector equation: \(x_1\overrightarrow{a_1}+x_2\overrightarrow{a_2}+\cdots+x_n\overrightarrow{a_n}=\overrightarrow{b}\), where \(A=[\overrightarrow{a_1}\:\overrightarrow{a_2}\:\cdots\overrightarrow{a_n}]\).

Example. \[\begin{eqnarray*} \begin{array}{rcrcrcr} &&2x_2 &-&8x_3&=&8\\ x_1&-&2x_2 &+&x_3&=&0\\ -4x_1&+&5x_2&+&9x_3&=&-9 \end{array} \end{eqnarray*}\] The matrix equation is \(A\overrightarrow{x}=\overrightarrow{b}\) where \[A=\left[\begin{array}{rrr}0&2&-8\\1&-2&1\\-4&5&9\end{array} \right],\; \overrightarrow{x}= \left[\begin{array}{c}x_1\\x_2\\x_3 \end{array} \right], \text{ and } \overrightarrow{b}= \left[\begin{array}{r}8\\0\\-9 \end{array} \right].\] The augmented matrix is \[ [A\:\overrightarrow{b}]=\left[\begin{array}{rrr|r}0&2&-8&8\\1&-2&1&0\\-4&5&9&-9\end{array} \right].\] The vector equation is \(x_1\left[\begin{array}{r}0\\1\\-4 \end{array} \right] +x_2\left[\begin{array}{r}2\\-2\\5 \end{array} \right] +x_3\left[\begin{array}{r}-8\\1\\9 \end{array} \right] =\left[\begin{array}{r}8\\0\\-9 \end{array} \right].\)
You may verify that one solution is \((x_1,x_2,x_3)=(29,16,3)\). Is it the only solution?

Last edited