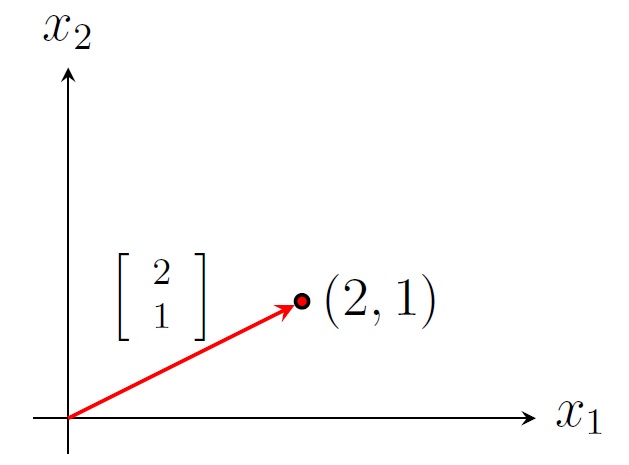
Position vector of a point in the 2-space \(\mathbb R^2\)
Matrix Operations |
Matrix: An \(m\times n\) matrix \(A\) is an \(m\)-by-\(n\) array of scalars from a field (for example
real numbers) of the form
\[A=\left[\begin{array}{cccc}
a_{11}&a_{12}&\cdots &a_{1n}\\
a_{21}&a_{22}&\cdots &a_{2n}\\
\vdots&\vdots&\ddots &\vdots\\
a_{m1}&a_{m2}&\cdots &a_{mn}
\end{array}\right].\]
The order (or size) of \(A\) is \(m\times n\) (read as m by n) if \(A\) has \(m\) rows and
\(n\) columns. The \((i,j)\)-entry of \(A=[a_{i,j}]\) is \(a_{i,j}\).
For example, \(A=\left[\begin{array}{rrr}1&2&0\\-3&0&-1\end{array} \right]\) is a \(2\times 3\) real matrix.
The \((2,3)\)-entry of \(A\) is \(-1\).
Equality: Two matrices \(A\) and \(B\) are equal, i.e., \(A=B\) if \(A\) and \(B\) have the same order
and the entries of \(A\) and \(B\) are the same.
Useful Matrices:

Position vector of a point in the 2-space \(\mathbb R^2\)
Matrix Operations:
Transpose: The transpose of an \(m\times n\) matrix \(A\), denoted by \(A^T\), is an \(n\times m\)
matrix whose columns are corresponding rows of \(A\), i.e., \((A^T)_{ij}=A_{ji}\).
Example.
If \(A=\left[\begin{array}{rrr}1&2&0\\-3&0&-1\end{array} \right]\), then \(A^T=\left[\begin{array}{rr}1&-3\\2&0\\0&-1\end{array} \right]\).
Properties: Let \(A\) and \(B\) be two matrices with appropriate orders. Then
Scalar Multiplication: Let \(A\) be a matrix and \(c\) be a scalar. The scalar multiple, denoted
by \(cA\), is the matrix whose entries are \(c\) times the corresponding entries of \(A\).
Example.
If \(A=\left[\begin{array}{rrr}1&2&0\\-3&0&-1\end{array} \right]\), then \(-2A=\left[\begin{array}{rrr}-2&-4&0\\6&0&2\end{array} \right]\).
Properties: Let \(A\) and \(B\) be two matrices of the same order and \(c\) and \(d\) be scalars. Then
Sum: If \(A\) and \(B\) are \(m\times n\) matrices, then the sum \(A+B\) is the \(m\times n\) matrix
whose entries are the sum of the corresponding entries of \(A\) and \(B\), i.e., \((A+B)_{ij}=A_{ij}+B_{ij}\).
Example.
If \(A=\left[\begin{array}{rrr}1&2&0\\-3&0&-1\end{array} \right]\) and \(B=\left[\begin{array}{rrr}0&-2&0\\3&0&2\end{array} \right]\),
then \(A+B=\left[\begin{array}{rrr}1&0&0\\0&0&1\end{array} \right]\).
Properties: Let \(A,B\), and \(C\) be three matrices of the same order. Then
Multiplication:
Matrix-vector multiplication: If \(A\) is an \(m\times n\) matrix and \(\overrightarrow{x}\) is an
\(n\)-dimensional vector, then their product \(A\overrightarrow{x}\) is an \(n\)-dimensional vector whose
\((i,1)\)-entry is \(a_{i1}x_1+a_{i2}x_2+\cdots+a_{im}x_n\), the dot product of the row \(i\) of \(A\) and
\(\overrightarrow{x}\). Note that
\[A\overrightarrow{x}=\left[\begin{array}{c}
a_{11}x_1+a_{12}x_2+\cdots+a_{1n}x_n\\
a_{21}x_1+a_{22}x_2+\cdots+a_{2n}x_n\\
\vdots\\
a_{m1}x_1+a_{m2}x_2+\cdots+a_{mn}x_n\end{array}\right]
=
x_1\left[\begin{array}{c}
a_{11}\\
a_{21}\\
\vdots\\
a_{m1}
\end{array}\right]+
x_2\left[\begin{array}{c}
a_{12}\\
a_{22}\\
\vdots\\
a_{m2}
\end{array}\right]+\cdots+
x_n\left[\begin{array}{c}
a_{1n}\\
a_{2n}\\
\vdots\\
a_{mn}
\end{array}\right].\]
Example.
If \(A=\left[\begin{array}{rrr}1&2&0\\-3&0&-1\end{array} \right]\) and
\(\overrightarrow{x}=\left[\begin{array}{r}1\\-1\\0\end{array} \right]\), then
\(A\overrightarrow{x}=\left[\begin{array}{r}-1\\-3\end{array} \right]\) which is a linear combination
of first and second columns of \(A\) with weights \(1\) and \(-1\) respectively.
Matrix-matrix multiplication: If \(A\) is an \(m\times n\) matrix and \(B\) is an \(n\times p\) matrix,
then their product \(AB\) is an \(m\times p\) matrix whose \((i,j)\)-entry is the dot product the row \(i\)
of \(A\) and the column \(j\) of \(B\).
\[(AB)_{ij}=a_{i1}b_{1j}+a_{i2}b_{2j}+\cdots+a_{im}b_{mj}\]
Example.
For \(A=\left[\begin{array}{rrr}1&2&2\\0&0&2\end{array} \right]\) and \(B=\left[\begin{array}{rr}2&-2\\0&0\\1&1\end{array} \right]\), we have
\(AB=\left[\begin{array}{rr}4&0\\2&2\end{array} \right].\)
Properties: Let \(A,B\), and \(C\) be three matrices of appropriate orders. Then
Remark.
Powers of a matrix:
If \(A\) is an \(n\times n\) matrix and \(k\) is a positive integer, then \(k\)-th power of \(A\), denoted by
\(A^k\), is the product of \(k\) copies of \(A\). We use the convention \(A^0=I_n\).
Example.
\(A=\left[\begin{array}{rr}0&1\\0&0\end{array} \right] \implies
A^2=AA=\left[\begin{array}{rr}0&0\\0&0\end{array} \right],\;
A^{100}=\left[\begin{array}{rr}0&0\\0&0\end{array} \right].\)
Symmetric and Skew-symmetric Matrices:
A square matrix \(A\) is symmetric if \(A^T=A\) and \(A\) is skew-symmetric if \(A^T=-A\).
A square matrix \(A\) can be written uniquely as a sum of a symmetric and a skew-symmetric matrix:
\[A=\frac{1}{2}\left(A+A^T \right)+\frac{1}{2} \left(A-A^T \right)\]
Example.
\[\left[\begin{array}{rr}1&4\\2&5\end{array}\right]
=\frac{1}{2}\left( \left[\begin{array}{rr}1&4\\2&5\end{array}\right] + \left[\begin{array}{rr}1&2\\4&5\end{array}\right] \right)
+\frac{1}{2}\left( \left[\begin{array}{rr}1&4\\2&5\end{array}\right] - \left[\begin{array}{rr}1&2\\4&5\end{array}\right] \right)
=\left[\begin{array}{rr}1&3\\3&5\end{array}\right]
+\left[\begin{array}{rr}0&1\\-1&0\end{array}\right].\]
Last edited