LearnMathOnline

Definition (Tree). A tree is a simple connected graph with no cycles. A graph is a forest if each of its connected components is a tree.

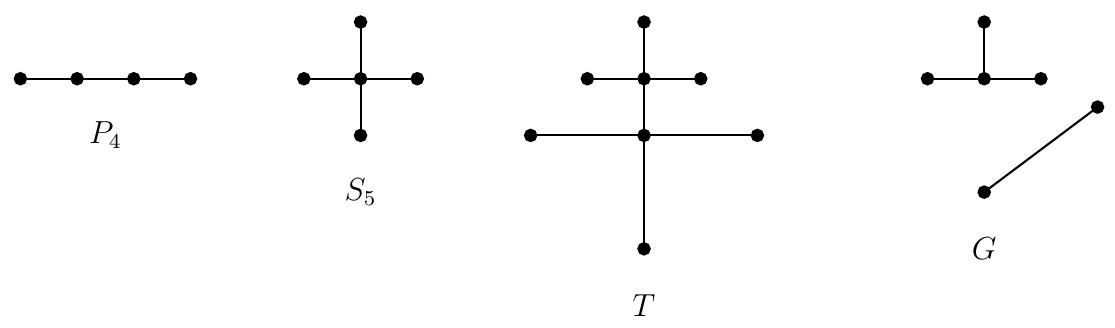
Example. \(P_4,\;S_5\), and \(T\) are trees and \(G\) is a forest.

Remark. In 1857, Aurther Caeley used trees to enumerate the isomers of saturated hydrocarbons \(C_nH_{2n+2}\). For example, butane \(C_4H_{10}\) has two isomers and they look like trees where atoms and atomic bonds represent vertices and edges respectively. Applications of trees include organizing a sequence of decisions and creating file directories in a computer and least expensive communication network.

Theorem. Let \(G\) be a simple graph on \(n\) vertices. Then the following are true.

(a) By induction on \(n\).

(b) Suppose there is a unique path between any two vertices in \(G\). Then \(G\) is connected. Conversely suppose that \(G\) is a tree. Then \(G\) is connected and consequently there is a path between any two vertices in \(G\). If there is more than one path between two vertices in \(G\), then \(G\) would have a cycle. Since \(G\), being a tree, has no cycles, there is a unique path between any two vertices in \(G\).

Corollary. A tree \(T\) with at least 2 vertices is a bipartite graph and hence \(\chi(T)=2\).

Fix a vertex \(v\) in \(T\) and color it red. Color vertex \(u\) blue if the unique path from \(v\) to \(u\) has odd length and red otherwise. Since there is no cycle in \(T\), there is no edge between two blue vertices or two red vertices. Thus blue vertices and red vertices form two partite sets of the bipartite graph \(T\) and consequently \(\chi(T)=2\).

Definition (Spanning tree). A spanning tree of a graph \(G\) is a subgraph that is a tree containing all the vertices of \(G\). A spanning forest of a graph \(G\) is a subgraph that is a forest containing all the vertices of \(G\).

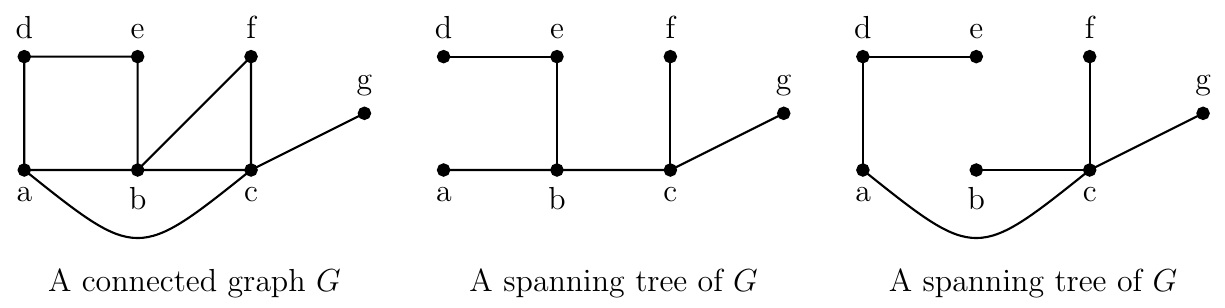
There may be a lot of spanning trees of a connected graph. Kirchhoff's theorem or matrix tree theorem provides the number of spanning trees in terms of nonzero eigenvalues of the Laplacian matrix of a graph.

Theorem (Matrix tree theorem). Let \(G\) be a simple graph on \(n\) vertices and \(L\) be the Laplacian matrix of \(G\) with eigenvalues \(0=\mu_1\leq \mu_2\leq \cdots \leq \mu_n\). Then the number \(t(G)\) of spanning trees of \(G\) is \[t(G)=\det\left(L(i)\right)=\frac{\mu_2\cdot \mu_3 \cdots \mu_n}{n},\] for all \(i=1,2,\ldots,n\).

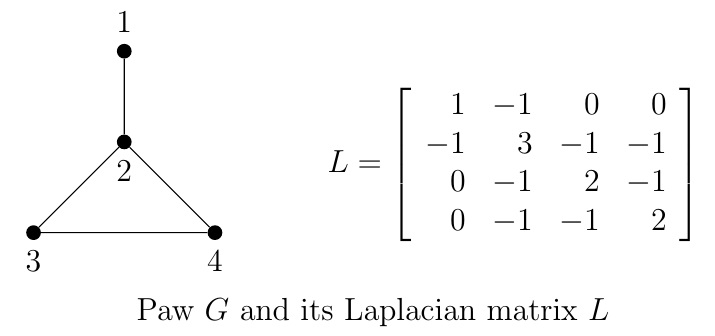
Example. The Laplacian matrix \(L\) of the paw graph \(G\) has eigenvalues \(0,1,3,4\). By matrix tree theorem, the number of its spanning trees is \[\det\left(L(2)\right)=\det \left[\begin{array}{rrr} 1&0&0\\ 0&2&-1\\ 0&-1&2 \end{array}\right]=\frac{1\cdot 3 \cdot 4}{4}=3.\] Remark. How do we find a spanning tree of a connected graph? Choose a cycle and delete one edge. Do it for all cycles, one at a time.

Problem. Find the number of edges whose removal from a connected graph \(G\) on \(n\) vertices and \(m\) edges produces a spanning tree of \(G\).

Solution. Let \(x\) be the required number of edges to be deleted to get a spanning tree of a connected graph \(G\) on \(n\) vertices and \(m\) edges. Since a spanning tree on \(n\) vertices has \(n-1\) edges, we have \(m-x=n-1\). Thus \(x=m-n+1\).

Theorem. A graph \(G\) is connected if and only if \(G\) has a spanning tree.

(\(\Longleftarrow\)) Suppose that \(G\) has a spanning tree \(T\). Then there a path between any two vertices of \(T\), hence of \(G\).

(\(\Longrightarrow\)) Suppose \(G\) is connected. If \(G\) has no cycles, \(G\) is a tree and hence a spanning tree of itself. Otherwise \(G\) has a cycle and delete one of its edges, say \(e\). Then \(G-e\) is still connected. By deleting edges of cycles of \(G\), one at a time, we end up with a connected graph with no cycles which is a spanning tree of \(G\).

Deleting edges from cycles to produce a spanning tree is inefficient as we have to identify cycles at each step. There are two better algorithms: depth-first search (backtracking) and breadth-first search. We illustrate breadth-first search by an example. First we need the following definition.

Definition (Rooted tree). A rooted tree is a tree in which one vertex is specified as the root. The level of a vertex \(v\) in a rooted tree is the length of the unique path from \(v\) to the root.

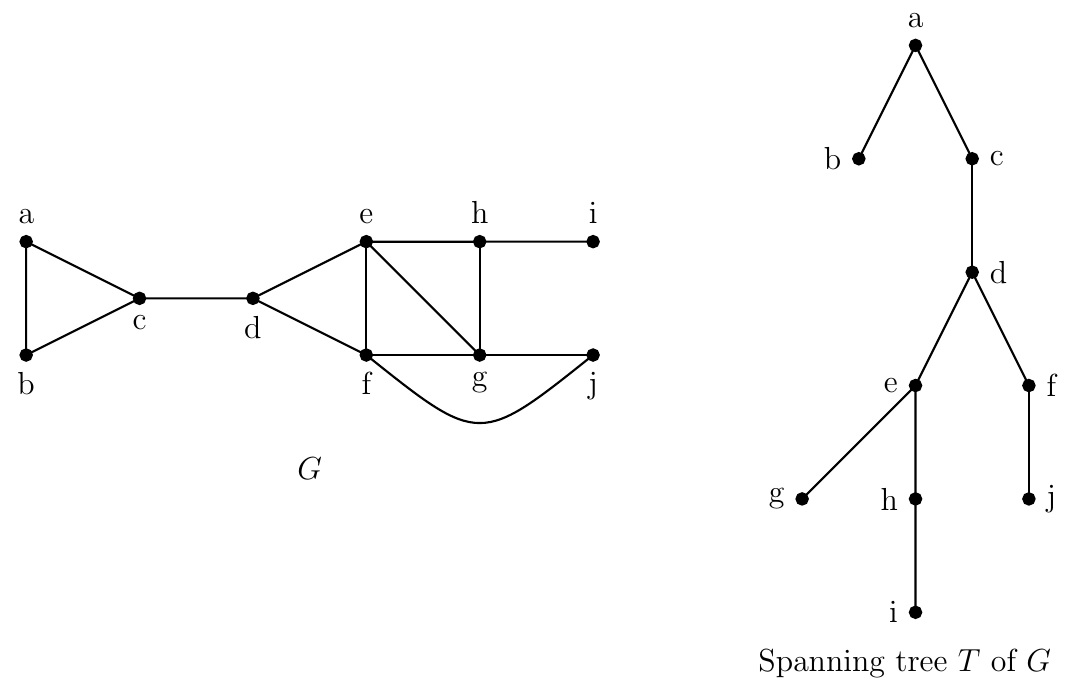
Problem. Use breadth-first search to produce a spanning tree \(T\) for the above graph \(G\). Choose \(a\) as the root of \(T\).

Solution. Start with vertex \(a\), the root. For the level 1 vertices, choose all the neighbors of \(a\) and add edges joining \(a\) and its neighbors. So we get \(b\) and \(c\) as the level 1 vertices (in alphabetical order) and edges \(\{a,b\}\) and \(\{a,c\}\).

For the level 2 vertices, choose all the neighbors of \(b\) and \(c\), that are not already chosen, and order them (alphabetically for this problem). For this graph, \(d\) is the only vertex in level 2. Join the first vertex in level 1, i.e., \(b\), and its neighbors in level 2. \(b\) is not adjacent to the only vertex \(d\) in level 2. Then join the second vertex in level 1, i.e., \(c\), and its neighbors in level 2 that are not already chosen. So we get \(\{c,d\}\).

For the level 3 vertices, choose all the neighbors of \(d\), that are not already chosen, and add edges joining \(d\) and its neighbors in level 3. So we get \(e\) and \(f\) as the level 3 vertices (in alphabetical order) and edges \(\{d,e\}\) and \(\{d,f\}\).

For the level 4 vertices, choose all the neighbors of \(e\) and \(f\), that are not already chosen, and order them. We get \(g\), \(h\), and \(j\) as the level 4 vertices. Join the first vertex in level 3, i.e., \(e\), and its neighbors in level 4. So we get \(\{e,g\}\) and \(\{e,h\}\). Then join the second vertex in level 3, i.e., \(f\), and its neighbors in level 4 that are not already chosen. So we get \(\{f,j\}\).

Continuing this process, we get \(\{h,i\}\) and a tree \(T\). Since tree \(T\) contains all the vertices of \(G\), \(T\) is a spanning tree of \(G\).

Trees