LearnMathOnline

Planar Graphs

Can we join three houses with three utilities so that none of the connections crosses? Note that the corresponding graph is \(K_{3,3}\). So can we draw \(K_{3,3}\) without edge-crossing?

Definition (Planar graph). A graph is planar if it can be drawn in the plane such that its edges intersect only at their endpoints (i.e., edges do not cross each other). A graph with such a drawing is called a planar embedding of the planar graph.

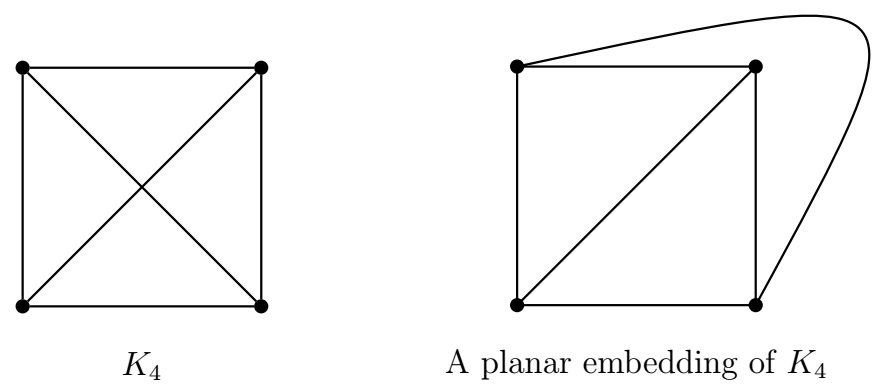
Example. \(K_4\) is a planar graph. \(K_5\) and \(K_{3,3}\) are not planar.

Definition (Face). A planar embedding of a planar graph splits the plane into regions called faces including an unbounded region called the outer face.

Example. The following planar embedding of \(K_4\) has 4 faces where face \(f_4\) is the outer face.

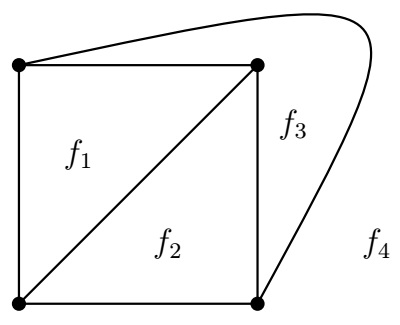
Theorem (Euler's formula). Let \(G\) be a simple connected planar graph on \(v\) vertices and \(e\) edges. If \(f\) is the number of faces in a planar embedding of \(G\), then \[v-e+f=2.\]

By induction on \(e\), the number of edges of \(G\).

Example. For \(K_4\), we have \(v=4\) and \(e=\binom{4}{2}=6\). By Euler's formula, the number of faces in a planar embedding of \(K_4\) is \[f=e-v+2=6-4+2=4.\]
Problem. Find the number of faces in a planar embedding of a \(3\)-regular connected planar graph \(G\) on 8 vertices.

Solution. Here \(v=8\) and the degree-sum is \(3\cdot 8=24\). So \[e=\frac{1}{2}(\text{the degree-sum})=\frac{1}{2}\cdot 24=12.\] By Euler's formula, the number of faces in a planar embedding of \(G\) is \[f=e-v+2=12-8+2=6.\]

Theorem. Let \(G\) be a simple connected planar graph on \(v\geq 3\) vertices and \(e\) edges. Then the following hold.

\(e\leq 3v-6\), and

\(e\leq 2v-4\) when \(G\) contains no \(C_3\).

Let \(f\) be the number of faces in a planar embedding of \(G\).

(a) The degree of a face \(f_i\), denoted by \(\operatorname{d}(f_i)\), is defined to be the number of edges on the boundary of \(f_i\). Since \(v\geq 3\), the degree of the outer face is at least 3. Since \(G\) has no loops or multiedges, \(\operatorname{d}(f_i)\geq 3\) for each face \(f_i\). Note that each edge is counted twice in the degree-sum of faces. Thus \[2e=\sum_{\text{face } f_i}\operatorname{d}(f_i).\] Since \(\operatorname{d}(f_i)\geq 3\) for each face \(f_i\), we have \[2e=\sum_{\text{face } f_i}\operatorname{d}(f_i)\geq 3f.\] Thus \(f\leq \frac{2}{3}e\). By Euler's formula, \(e-v+2=f\leq \frac{2}{3}e\). Thus \(\frac{1}{3}e\leq v-2\) which implies \(e\leq 3v-6\).

(b) Similar proof.

Problem. Use an upper bound of the number of edges of a planar graph to prove that \(K_5\) and \(K_{3,3}\) are not planar graphs.

Solution. For \(K_5\), \(v=5\) and \(e=\binom{5}{2}=10\). Suppose that \(K_5\) is planar. Then by the above theorem, \(10=e\leq 3v-6=3\cdot5-6=9\), a contradiction. Thus \(K_5\) is not a planar graph.

For \(K_{3,3}\), \(v=6\) and \(e=3\cdot3=9\). Since \(K_{3,3}\) is a bipartite graph, it has no odd cycles. Suppose that \(K_{3,3}\) is planar. Then by the above theorem, \(9=e\leq 2v-4=2\cdot6-4=8\), a contradiction. Thus \(K_{3,3}\) is not a planar graph.

Problem. Prove that if \(G\) is a simple connected planar graph, then \(G\) has a vertex of degree at most 5.

Solution. Let \(v\) and \(e\) be the number of vertices and edges of a simple connected planar graph \(G\) respectively. If \(v=1 \text{ or } 2\), then the result is true. Suppose \(v\geq 3\). Then by (a) of the preceding theorem, \(e\leq 3v-6\). Suppose \(\operatorname{d}(x)\geq 6\) for all vertices \(x\) of \(G\). Then \[e=\frac{1}{2}\sum_{\text{vertex }x}\operatorname{d}(x)\geq \frac{1}{2}(6v)=3v\] which contradicts the fact that \(e\leq 3v-6 < 3v\).

Definition (Subdivision). A subdivision of an edge \(\{u,v\}\) is the path \(uvw\) obtained by inserting a new vertex \(w\) on the edge \(\{u,v\}\). A subdivision of a graph \(G\) is obtained from \(G\) by subdivision of edges in \(G\).

Remark. A graph \(G\) is planar if and only if every subdivision of \(G\) is planar.

Theorem (Kuratowski, 1930). A graph is planar if and only if it does not contain a subdivision of \(K_5\) or \(K_{3,3}\).

(\(\Longrightarrow\)) Since \(K_5\) or \(K_{3,3}\) are nonplanar, their subdivisions are also nonplanar. Thus if a graph is planar, then it does not contain a subgraph that is a subdivision of \(K_5\) or \(K_{3,3}\).
(\(\Longleftarrow\)) Nontrivial proof.

Remark. Applications of planar graphs include designing road networks without underpasses or overpasses and designing electronic circuits on a board without insulated wires. There are interesting topics related to planar graphs such as thickness, crossing number, graph embedding on surfaces (see topological graph theory).

Last edited