Two graphs with different drawings may have the same graph properties. How do we know two graphs are essentially the same but with different labelings of vertices?

Definition (Isomorphism). Two simple graphs \(G=(V_G,E_G)\) and \(H=(V_H,E_H)\) are isomorphic, denoted by \(G\cong H\), if there is a bijection (one-to-one and onto function) \(f:V_G\to V_H\) such that \(\{a,b\}\in E_G\) if and only if \(\{f(a),f(b)\}\in E_H\). Such a function \(f\) is called an isomorphism between \(G\) and \(H\). If there is an isomorphism between \(G\) and \(H\), they are called isomorphic. Two graphs are nonisomorphic if they are not isomorphic.

Remark. A property of graphs preserved under graph isomorphism are called a graph invariant. For example, the number of vertices and edges, degree sequence, connectedness, vertex connectivity, chromatic number are graph invariants.

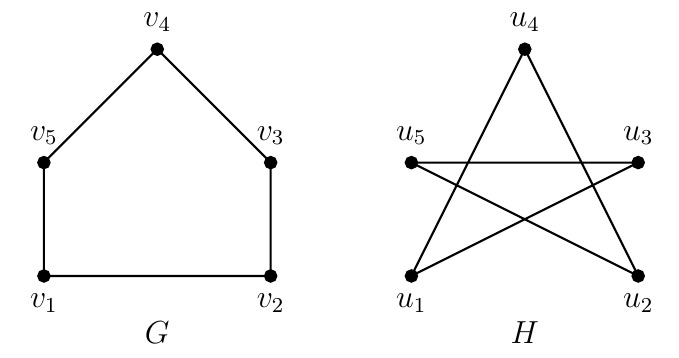
Problem. Determine whether \(G\) and \(H\) are isomorphic. Find an isomorphism or provide a rigorous argument that none exists.

Solution. Consider the bijection \(f:V(G)\to V(H)\) such that \[f(v_1)=u_1,\;f(v_2)=u_3,\;f(v_3)=u_5,\;f(v_4)=u_2, \text{ and } f(v_5)=u_4.\] It can be verified that \(\{v_i,v_j\}\in E(G)\) if and only if \(\{f(v_i),f(v_j)\}\in E(H)\). Thus \(G\cong H\), i.e., \(G\) and \(H\) are isomorphic.

Problem. Determine whether \(G\) and \(H\) are isomorphic. Find an isomorphism or provide a rigorous argument that none exists.

Solution. Suppose there is an isomorphism \(f:V(G)\to V(H)\). Since \(\operatorname{d}(v_1)=1\) and \(\operatorname{d}(u_1)=\operatorname{d}(u_7)=\operatorname{d}(u_8)=\operatorname{d}(u_6)=1\), \(f(v_1)\) is one of \(u_1,u_6,u_7\), and \(u_8\). Note that \(v_1\) is adjacent to \(v_2\) which has degree 2. But none of \(u_1,u_6,u_7\), and \(u_8\) is adjacent to a degree 2 vertex. Thus there is no such isomorphism \(f:V(G)\to V(H)\), i.e., \(G\) and \(H\) are not isomorphic. Note that \(G\) and \(H\) have the same degree sequence \((3,3,2,2,1,1,1,1)\).

Definition. A permutation matrix of order \(n\) is a binary matrix obtained from the identity matrix \(I_n\) by permuting (i.e., rearranging) its rows.

Theorem. Two simple graphs \(G\) and \(H\) are isomorphic if and only if \(A_H=PA_GP^T\) for some permutation matrix \(P\).

Example.

For the above isomorphic graphs \(G\) and \(H\), \(A_H=PA_GP^T\), i.e., \[\left[\begin{array}{ccccc} 0&0&1&1&0\\ 0&0&0&1&1\\ 1&0&0&0&1\\ 1&1&0&0&0\\ 0&1&1&0&0 \end{array}\right] =\left[\begin{array}{ccccc} 1&0&0&0&0\\ 0&0&0&1&0\\ 0&1&0&0&0\\ 0&0&0&0&1\\ 0&0&1&0&0 \end{array}\right] \left[\begin{array}{ccccc} 0&1&0&0&1\\ 1&0&1&0&0\\ 0&1&0&1&0\\ 0&0&1&0&1\\ 1&0&0&1&0 \end{array}\right] \left[\begin{array}{ccccc} 1&0&0&0&0\\ 0&0&1&0&0\\ 0&0&0&0&1\\ 0&1&0&0&0\\ 0&0&0&1&0 \end{array}\right]. \] Note that \(P=\left[\begin{array}{ccccc} 1&0&0&0&0\\ 0&0&0&1&0\\ 0&1&0&0&0\\ 0&0&0&0&1\\ 0&0&1&0&0 \end{array}\right]\) is obtained from \(I_5\) by permuting rows \(1,2,3,4,5\) to rows \(1,3,5,2,4\) respectively which is seen from the isomorphism \(f:V(G)\to V(H)\): \[f(v_1)=u_1,\;f(v_2)=u_3,\;f(v_3)=u_5,\;f(v_4)=u_2, \text{ and } f(v_5)=u_4.\]

Remark. There are \(n!\) possible isomorphisms between two graphs on \(n\) vertices. The graph isomorphism problem is to determine whether two given graphs on \(n\) vertices are isomorphic. The graph isomorphism problem is a famous problem in computational complexity and it is not known whether it is solvable in polynomial time (i.e., the number of steps is a polynomial of \(n\)).

Last edited