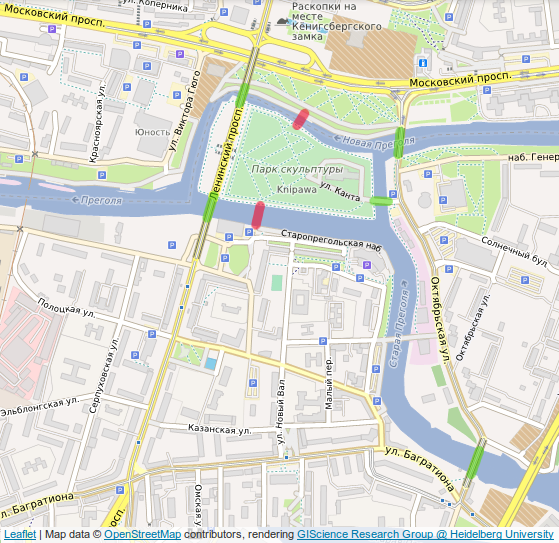
The seven bridges of Königsberg
The city of Königsberg, Prussia (now Kaliningrad, Russia) is divided into four parts by the branches of Pregel river. The problem was to find a walk that starts at some location of the city, crosses each bridge exactly once, and returns to the starting point.

Photo: Wikipedia

In 1736, Leonard Euler converted the problem in terms of vertices (points or nodes) and edges (lines or links). He proved that no such walk exists. His work laid to the foundation of graph theory.

A graph corresponding to the seven bridges of Königsberg problem

Definition (Graph). A graph is an ordered pair \(G=(V,E)\) consisting of a non-empty set \(V\) of vertices and a multiset \(E\) of edges which are unordered pairs of vertices in \(V\).

Example. In the preceding graph \(G=(V,E)\), \(V=\{1,2,3,4\}\) and \[E=\{\{4,1\},\{4,2\},\{4,3\},\{1,2\},\{1,2\},\{1,3\},\{1,3\}\}.\] This graph is a multigraph because it has multiple edges between two vertices, e.g., \(1\) and \(2\).

Definition (Simple graph). A graph is a simple graph if it has no multiedges and no loops (edges of the form \(\{v,v\}\) for some vertex \(v\)).

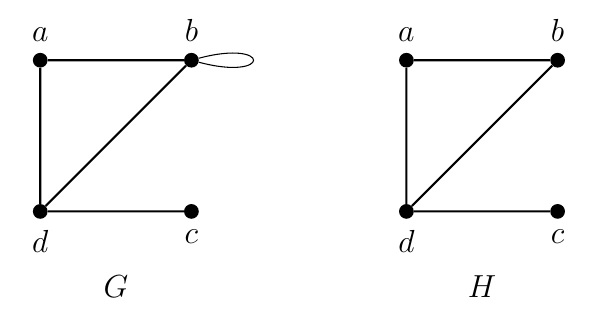
Example. The preceding graph \(G\) is not a simple graph because of its loop \(\{b,b\}\). But graph \(H\) is a simple graph.

Remark. Two vertices \(u\) and \(v\) are called adjacent if there is an edge \(e=\{u,v\}\) between them. We call \(e=\{u,v\}\) to be incident with \(u\) and \(v\).

When the edges of a graph are directed, they are called arcs and the graph is called a directed graph or digraph.

Definition (Digraph). A digraph is an ordered pair \(G=(V,A)\) consisting of a non-empty set \(V\) of vertices and a multiset \(A\) of arcs which are ordered pairs of vertices in \(V\) (i.e., \(A\subseteq V\times V\)).

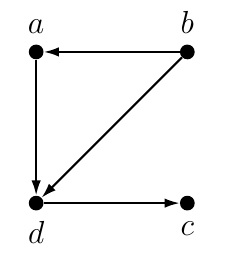
Example. In the preceding digraph \(G=(V,A)\), \(V=\{a,b,c,d\}\) and \[A=\{(a,d),(b,a),(b,d),(d,c)\}.\] Note that digraph \(G\) is a webgraph for webpages a,b,c, and d where an arc represents a hyperlink on one webpage pointing to another. For example, arc \((b,a)\) indicates that there is a hyperlink on webpage \(b\) pointing to webpage \(a\). We can rank the webpages for their importance by PageRank algorithm.

Remark. For an arc \((a,b)\), \(a\) is called the initial vertex and \(b\) is called the terminal vertex.

Last edited