Recall the seven bridges of Königsberg problem: Can we cross all the 7 bridges exactly once and come back to the starting point? In other words, is there a circuit in the corresponding graph containing each of its edges exactly once?

A graph corresponding to the seven bridges of Königsberg problem

Definition (Euler circuit). An Euler walk in in a connected graph \(G\) is a walk that visits each edge of \(G\) exactly once. An Euler circuit in a connected graph \(G\) is a circuit (i.e., closed walk) that visits each edge of \(G\) exactly once. A graph \(G\) is Eulerian if it contains an Euler circuit.

Theorem. A connected graph with at least 2 vertices has an Euler circuit if and only if each of its vertex has even degree.

Theorem. A connected graph with at least 2 vertices has an Euler walk but not a Euler circuit if and only if it has exactly 2 vertices of odd degree.

Example. Determine whether the following graphs have an Euler circuit or an Euler walk.

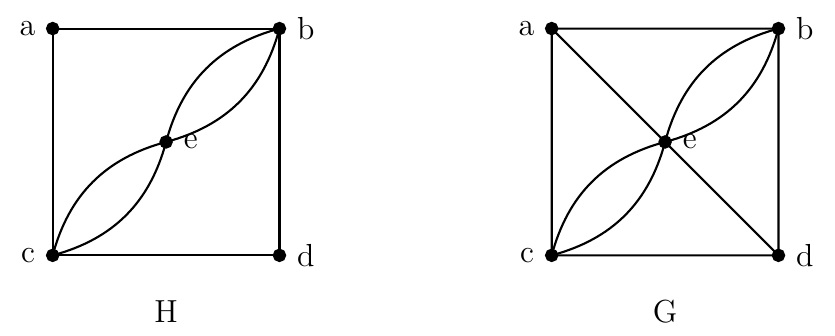
Solution. Since the degree of each vertex of \(H\) is even, \(H\) has a Euler circuit, for example, \(abdcebeca\). Since \(\operatorname{d}(a)=3\) is odd, \(G\) has no Euler circuit. Note that \(\operatorname{d}(a)=\operatorname{d}(d)=3\), \(\operatorname{d}(b)=\operatorname{d}(c)=4\), and \(\operatorname{d}(e)=6\). Since \(G\) has exactly two vertices of odd degree, \(G\) has an Euler walk from \(a\) to \(d\): \(aecebedbacd\).

Definition (Hamilton circuit). A Hamilton walk in a connected graph \(G\) is a walk that passes through each vertex of \(G\) exactly once. A Hamilton circuit in a connected graph \(G\) is a circuit that passes through each vertex of \(G\) exactly once.

Example. \(K_2\) has a Hamilton walk but no Hamilton circuit. \(K_n,n\geq 3\) has \(\frac{(n-1)!}{2}\) Hamilton circuits.

Remark. Note that unlike an Euler circuit there are no necessary and sufficient conditions for existence of a Hamilton circuit. But we have some sufficient conditions in terms of enough edges.

Theorem (Dirac's Theorem, 1952). Let \(G\) be a simple graph on \(n\geq 3\) vertices. If each vertex of \(G\) has degree at least \(\frac{n}{2}\), then \(G\) has a Hamilton circuit.

Theorem (Ore's Theorem, 1960). Let \(G\) be a simple graph on \(n\geq 3\) vertices. If \(\operatorname{d}(u)+\operatorname{d}(v)\geq n\) for any two non-adjacent vertices \(u\) and \(v\) of \(G\), then \(G\) has a Hamilton circuit.

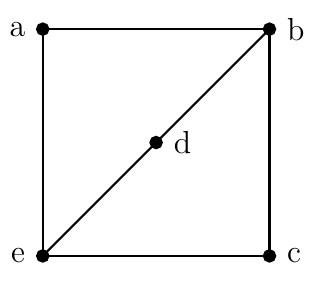
Example. The following graph has a Hamilton circuit \(abcdea\). But it does not satisfy the condition of Dirac's Theorem because \(\operatorname{d}(a)=2\not\geq \frac{5}{2}\). Also it does not satisfy the condition of Ore's Theorem because \(\operatorname{d}(a)+\operatorname{d}(c)=4\not\geq 5\).

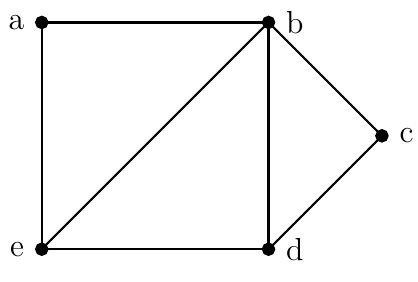
Example. The following graph has no Hamilton circuits. But it has a Hamilton walk \(abced\).

The Travelling Salesman Problem (TSP):
Consider a weighted graph (edges have weights). Find a circuit that passes through each vertex exactly once where the sum of weights of corresponding edges is minimum, i.e., find a Hamilton circuit with minimum weight. This appears in planning, logistics, microchips manufacturing, and DNA sequencing. How hard is it to find a Hamilton circuit? NP-hard (Further reading: computational complexity).

Last edited