Definition (Chromatic number).
A (proper) coloring of a graph is to assign colors to vertices of the graph so that any two adjacent vertices
get different colors. A graph is \(k\)-colorable if it has a coloring with \(k\) colors. The chromatic number of
a graph \(G\), denoted by \(\chi(G)\), is the minimum number of colors needed for a coloring of \(G\). A graph \(G\) is
\(k\)-chromatic if \(\chi(G)=k\).
Example.
Chromatic numbers of some well-known graphs.
\(\chi(G)=1\) if and only if \(G\) has no edges.
\(\chi(K_n)=n\).
\(\chi(C_n)=\begin{cases}
2 & \text{if } n\text{ is even}\\
3 & \text{if } n\text{ is odd.}
\end{cases}\)
\(\chi(P_n)=\chi(S_n)=\chi(K_{m,n})=2\).
\(\chi(G)=2\) if and only if \(G\) is bipartite.
Remark. Applications of graph colorings include scheduling final exams, frequency assignment for TV channels etc.
Definition (Clique number).
The clique number of a graph \(G\), denoted by \(\omega(G)\), is the number of vertices in a largest clique
(i.e., complete graph) in \(G\).
The maximum degree of a vertex in a graph \(G\) is denoted by \(\Delta(G)\).
Theorem.
For a graph \(G\), \(\omega(G) \leq \chi(G)\leq \Delta(G)+1.\)
Since \(K_{\omega(G)}\) is a subgraph of \(G\) and \(\chi(K_{\omega(G)})=\omega(G)\), we have
\[\omega(G)=\chi(K_{\omega(G)})\leq \chi(G).\]
Consider the following greedy coloring of all the vertices \(v_1,v_2,\ldots,v_n\) of \(G\) with colors
\(c_1,c_2,\ldots,c_{\Delta(G)+1}\): color vertex \(v_i\) with the first available color, i.e., \(c_j\) for the smallest \(j\)
that was not used to color neighbors of \(v_i\) among \(v_1,v_2,\ldots,v_{i-1}\). Note that when \(v_i\) is colored,
the number of its neighbors already colored is no greater than its degree \(\operatorname{d}(v_i)\).
Thus \(\chi(G)\leq \Delta(G)+1\).
Remark.
Note that \(\chi(G)=\Delta(G)+1\) if \(G\) is \(K_n\) or an odd cycle. Otherwise \(\chi(G)\leq \Delta(G)\) as stated by Brooks' theorem.
Theorem (Brooks' theorem).
\(\chi(G)\leq \Delta(G)\) for any connected graph \(G\) that is neither a complete graph nor an odd cycle.
Question.
How many colors are needed to color all the countries in a map so that two countries with a common border get different colors?
What is the chromatic number of the dual of a planar graph?
Definition (Dual graph).
Consider a planar embedding \(G\) of a planar graph. The dual of \(G\), denoted by \(G^*\), is the graph whose vertices are the faces of \(G\)
such that there is an edge \(e^*\) between two distinct vertices (faces of \(G\)) of \(G^*\) if and only if their corresponding faces in \(G\) are separated
by an edge \(e\) of \(G\)
where \(G^*\) has a loop corresponding to a face of \(G\) on both side of a cut edge in \(G\).
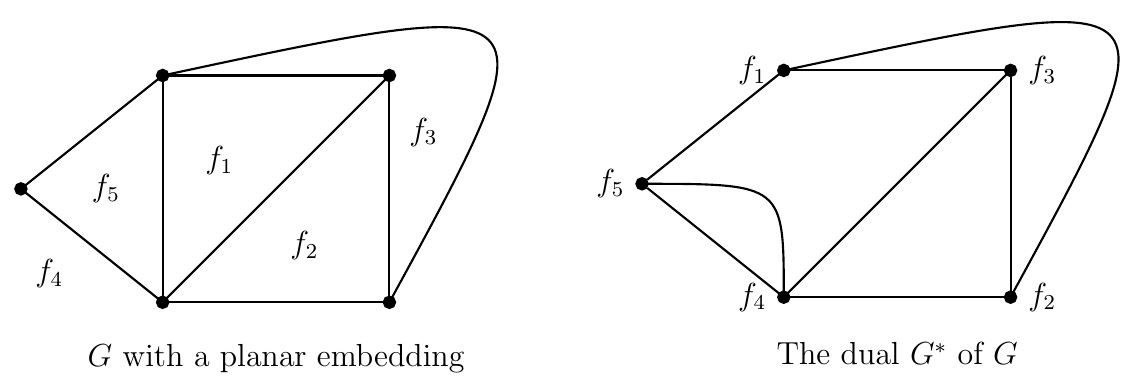
Example.
The above graph \(G\) with a planar embedding has five faces \(f_1,f_2,f_3,f_4,f_5\) which are the vertices of \(G^*\), the dual of \(G\).
Note that face \(f_1\) and the outer face \(f_4\) do not have any common edge on their boundaries which implies there is no edge between
\(f_1\) and \(f_4\) in \(G^*\). There are two edges between \(f_4\) and \(f_5\) in \(G^*\) because faces \(f_4\) and \(f_5\) are separated by two edges in \(G\).
Remark.
The dual of a planar embedding of a planar graph is a connected planar graph (see the above example).
Also note that for a planar embedding \(G\) of any connected planar graph, \(G^{**}\cong G\).
Example.
For the above graph \(G\) and its dual \(G^*\), note that \(\chi(G)=4\) and \(\chi(G^*)= 3\). Since \(\chi(G^*)= 3\), we need minimum 3 colors to color faces of \(G\) such that any two faces with a common edge on their boundaries get different colors.
Theorem (The four color theorem). Every planar graph without loops is 4-colorable, i.e., if \(G\) is a loopless planar graph, then \(\chi(G)\leq 4\).
Remark.
By the four color theorem, we need at most four colors to color all the countries in a map so that two countries with a common border get different colors.
The four color theorem was conjectured by 21 year old Francis Guthrie (an ex-student of Augustus De Morgan) in 1852. After lots of incorrect proofs by many people,
Appel and Haken proved it in 1976 by studying possible 1936 minimal counterexamples by computers. There is still no proof that does not use computers.
