Definition (Bipartite graph).
A bipartite graph is a graph whose vertex set can be partitioned into two sets \(V_1\) and \(V_2\) (called partite sets)
such that each of its edges joins a vertex \(V_1\) with a vertex of \(V_2\).
Example.
\(K_{m,n}\), the complete bipartite graph on \(m+n\) vertices, is the simple graph whose vertex set is partitioned into
two sets \(V_1\) and \(V_2\) such that \(|V_1|=m\), \(|V_2|=n\), and each vertex \(V_1\) is adjacent with each vertex of \(V_2\).
Note that \(|E(K_{m,n})|=mn\).
\(S_n\), the star on \(n\geq 3\) vertices, is the complete bipartite graph \(K_{1,n-1}\).
An even cycle, i.e., \(C_n\) with even \(n\), is a bipartite graph. But odd cycles are not bipartite graphs.
Definition (Subgraph).
A subgraph of a graph \(G=(V,E)\) is a graph \(H\) whose vertex set \(V(H)\) is a subset of \(V\) and edge set \(E(H)\) is a subset of \(E\).
A subgraph \(H\) of \(G\) is an induced subgraph of \(G\) induced by the vertex set \(W\) if its vertex set is \(V(H)=W\) and
edge set \(E(H)\) is the set of all edges in \(G\) that have both endpoints in \(V(H)=W\).
Example.
\(K_{1,2}\) and \(K_{2,2}=C_4\) are induced subgraphs of \(K_{2,3}\). \(5K_1\) and \(2K_2\) are subgraphs (not induced subgraphs) of \(K_{2,3}\).
Theorem.
A graph is bipartite if and only if it does not contain an odd cycle as a subgraph.
Suppose graph \(G\) is bipartite with partite sets \(V_1\) and \(V_2\). Let cycle \(C_k\) be a subgraph of \(G\) with edges
\[\{x_1,x_2\},\;\{x_2,x_3\},\ldots,\{x_{k-1},x_k\},\;\{x_k,x_1\}.\]
Without loss of generality, let \(x_1\in V_1\). Since \(G\) is bipartite and \(\{x_1,x_2\}\) is an edge of \(G\), \(x_2\in V_2\).
Similarly \(x_i\in V_2\) for all even \(i\in \{1,2,\ldots,k\}\). If \(k\) is odd, then \(x_k\in V_1\) which (because of the edge
\(\{x_k,x_1\}\)) implies \(x_1\in V_2\), a contradiction. Thus \(k\) is even and \(C_k\) is an even cycle. The converse will be proved later
with the notion of distance between vertices.
Definition (Matching).
A matching of a graph \(G\) is a set of vertex-disjoint non-loop edges of \(G\). Each vertex in a matching \(M\) is called
matched by \(M\) and \(M\) is said to match each vertex of \(M\). A matching \(M\) of \(G\) is a perfect matching
if each vertex of \(G\) is matched by \(M\).
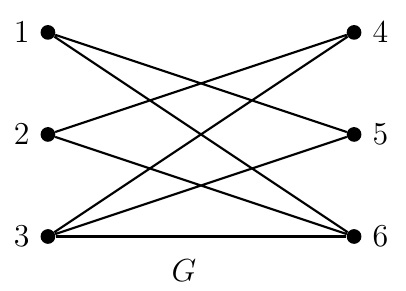
Example.
Each of vertices \(1,3,5,6\) of the preceding bipartite graph \(G\) is matched by matchings \(\{\{1,5\},\{3,6\}\}\) and \(\{\{1,6\},\{3,5\}\}\).
Note that \(\{\{1,5\},\{2,4\},\{3,6\}\}\) and \(\{\{1,6\},\{2,4\},\{3,5\}\}\) are perfect matchings of \(G\)
Remark.
A graph with a perfect matching has even number of vertices. A necessary and sufficient condition for a graph to have a perfect matching is
given by Tutte's theorem in terms of certain connected components of the graph.
Definition (Neighborhood).
The neighborhood of a vertex set \(W\) in a graph \(G\), denoted by \(\operatorname{N}(W)\), is the set of all vertices in \(G\)
that are adjacent with some vertex in \(W\). For a vertex \(v\) in \(G\), \(\operatorname{N}(\{v\})\) is simply denoted by
\(\operatorname{N}(v)\).
Example.
In the preceding graph \(G\), \(\operatorname{N}(1)=\{5,6\}\) and \(\operatorname{N}(\{1,5\})=\{1,3,5,6\}\).
Theorem (Hall's marriage theorem, 1935).
Let \(G\) be a bipartite graph with partite sets \(V_1\) and \(V_2\). There is a matching \(M\) of \(G\) for which each vertex of \(V_1\)
is matched by \(M\) if and only if for all subsets \(S\subseteq V_1\),
\[|S|\leq |N(S)|.\]
Suppose there is a matching \(M\) of \(G\) for which each vertex of \(V_1\) is matched by \(M\). Let \(S\subseteq V_1\). Each vertex of \(S\)
is adjacent to a vertex in \(V_2\) via an edge in \(M\). Since the edges of \(M\) are vertex-disjoint, \(|S|\leq |N(S)|\).
Conversely suppose \(|S|\leq |N(S)|\) for all subsets \(S\subseteq V_1\). We can find a matching \(M\) of \(G\) that matches each vertex of
\(V_1\) by strong induction on \(|V_1|\) (details skipped).
Remark.
To see the preceding theorem in terms of marriage, consider \(m\) men and \(n\) women where each of these \(m\) men has a subset of these \(n\)
women acceptable as a spouse and each of these \(n\) women would marry a man who wants to marry her. Is it possible that all of the \(m\) men
can be married? The answer is yes if and only if for any subset \(S\) of men, the number of their possible spouses is bigger than \(|S|\).
