Note that the statement is true for \(k=1\) because the \((i,j)\)-entry of \(A\) is \(1\) if and only if there is an edge between \(v_i\) and \(v_j\).
Prove by induction on \(k\).
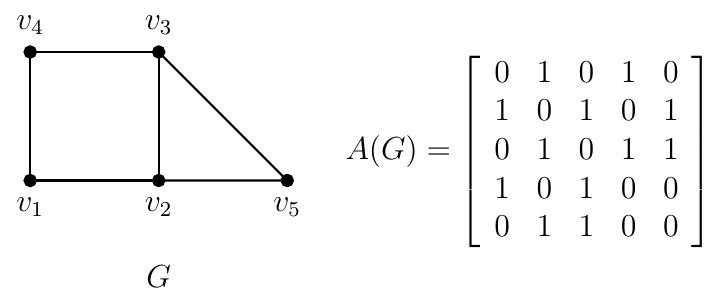
Adjacency and Incidence Matrices |
How to store information about a given graph \(G\)? Is there any alternative way to represent \(G\) rather than writing its vertex set and edge set?
Definition (Adjacency matrix).
Let \(G\) be a simple graph on \(n\) vertices \(v_1,v_2,\ldots,v_n\). The adjacency matrix \(A=[a_{ij}]\) of \(G\) is the \(n\times n\) binary matrix
such that
\[a_{ij}=\begin{cases}
1 & \text{if } \{v_i,v_j\}\text{ is an edge in } G\\
0 & \text{otherwise.}
\end{cases}\]
Sometimes it is denoted by \(A(G)\) or \(A_G\).
Example.
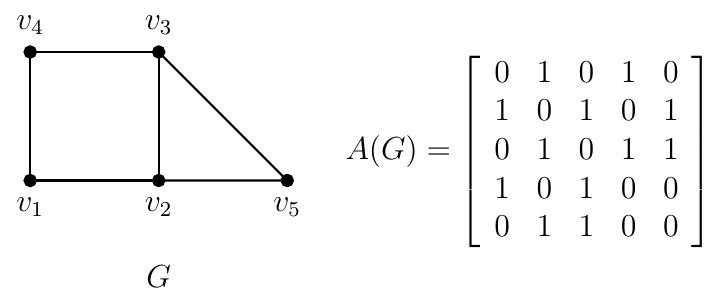
Remark.
If \(G\) is a simple digraph, then the \((i,j)\)-entry of its adjacency matrix \(A=[a_{ij}]\) is \(1\) if and only if \((v_i,v_j)\) is an arc in \(G\).
Problem.
What is the sum of entries in a row (column) of the adjacency matrix \(A\) of a simple graph \(G\)? What if \(G\) is a simple digraph?
Solution. If \(G\) is a simple graph, then the sum of entries of row (column) \(i\) of \(A\) is \(\operatorname{d}(v_i)\), the degree of
the vertex \(v_i\). If \(G\) is a simple digraph, then the sum of entries of row \(i\) of \(A\) is the out-degree of the vertex \(v_i\) and
the sum of entries of column \(i\) of \(A\) is the in-degree of the vertex \(v_i\).
Theorem.
Let \(G\) be a simple graph on \(n\) vertices \(v_1,v_2,\ldots,v_n\) with the adjacency matrix \(A\). The number of walks of length \(k\) from \(v_i\) to
\(v_j\) is the \((i,j)\)-th entry of \(A^k\).
Example. For the adjacency matrix \(A\) of the graph in the above example, \[A^2=\left[\begin{array}{ccccc} 2&0&2&0&1\\ 0&3&1&2&1\\ 2&1&3&0&1\\ 0&2&0&2&1\\ 1&1&1&1&2 \end{array}\right],\; A^3=\left[\begin{array}{ccccc} 0&5&1&4&2\\ 5&2&6&1&4\\ 1&6&2&5&4\\ 4&1&5&0&2\\ 2&4&4&2&2 \end{array}\right].\] Note that \((A^2)_{13}=2\) and there are 2 walks of length \(2\) from \(v_1\) to \(v_3\): \(v_1v_2v_3\) and \(v_1v_4v_3\). The diagonal entries of \(A^2\) are the degrees of the vertices. Also \((A^3)_{12}=5\) and there are 5 walks of length \(3\) from \(v_1\) to \(v_2\): \[ v_1v_4v_3v_2, v_1v_4v_1v_2, v_1v_2v_5v_2, v_1v_2v_3v_2, v_1v_2v_1v_2. \]
Definition (Incidence matrix). Let \(G\) be a simple graph with \(n\) vertices \(v_1,v_2,\ldots,v_n\) and \(m\) edges \(e_1,e_2,\ldots,e_m\). The incidence matrix \(M=[m_{ij}]\) of \(G\) is the \(n\times m\) binary matrix such that \[m_{ij}=\begin{cases} 1 & \text{if } e_j\text{ is incident with } v_i\\ 0 & \text{otherwise.} \end{cases} \] Example.
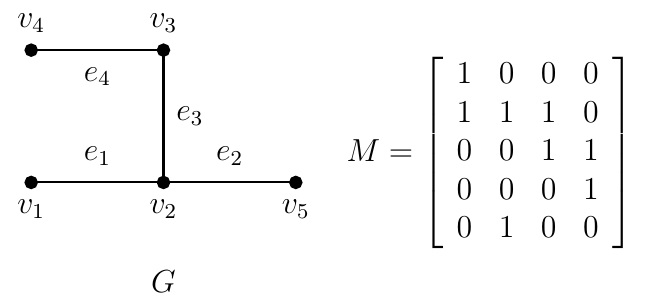
Problem.
What is the sum of entries in a row and column of the incidence matrix \(M\) of a simple graph \(G\)?
Solution. If \(G\) is a simple graph, then the sum of entries of row \(i\) of \(M\) is \(\operatorname{d}(v_i)\), the degree of the vertex \(v_i\)
and the sum of entries of each column of \(M\) is \(2\).
Definition (Laplacian matrix).
Let \(G\) be a simple graph on \(n\) vertices \(v_1,v_2,\ldots,v_n\) with the adjacency matrix \(A\). The degree matrix of \(G\) is the \(n\times n\)
diagonal matrix \(D=[d_{ij}]\) such that \(d_{ii}=\operatorname{d}(v_i)\) for \(i=1,2,\ldots,n\). The Laplacian matrix of \(G\), denoted by \(L\),
is \(L=D-A\). The signless Laplacian matrix of \(G\), denoted by \(Q\), is \(Q=D+A\).
Example.
For the above graph \(G\),
\[D=\left[\begin{array}{ccccc}
1&0&0&0&0\\
0&3&0&0&0\\
0&0&2&0&0\\
0&0&0&1&0\\
0&0&0&0&1
\end{array}\right],\;
A=\left[\begin{array}{ccccc}
0&1&0&0&0\\
1&0&1&0&1\\
0&1&0&1&0\\
0&0&1&0&0\\
0&1&0&0&0
\end{array}\right],\]
\[
L=D-A=\left[\begin{array}{rrrrr}
1&-1&0&0&0\\
-1&3&-1&0&-1\\
0&-1&2&-1&0\\
0&0&-1&1&0\\
0&-1&0&0&1
\end{array}\right],\]
\[Q=D+A=\left[\begin{array}{ccccc}
1&1&0&0&0\\
1&3&1&0&1\\
0&1&2&1&0\\
0&0&1&1&0\\
0&1&0&0&1
\end{array}\right].
\]
Observation.
Let \(G\) be a simple graph with the Laplacian Matrix \(L\), signless Laplacian Matrix \(Q\), and incidence matrix \(M\).
Last edited